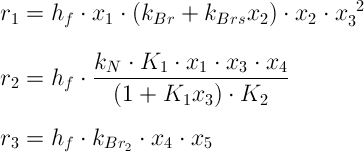
Spectacular fast reaction with delay, mathematical description

This webpage describes a very interesting and remarkable reaction. It is not the reactants and products which are remarkable, but it is the dynamics of the reaction which is striking. This experiment involves mixing two solutions and when this is done, then for tens of seconds or even a few minutes nothing seems to happen and after that, there suddenly is a really spectacular transition from seemingly no reaction at all to near explosive violence. The transition is really spectacular and the long induction time makes it very special, much more so than an equally violent reaction which occurs immediately, or which is the climax of a runaway-type of reaction which slowly becomes more and more violent over time.

The experiment is very simple. Simply mix a concentrated solution of hydroxyl ammonium chloride with a concentrated solution of sodium bromate and wait. Another option is to add a concentrated solution of hydroxyl ammonium chloride to some solid sodium bromate.

In this webpage, it is shown by means of high speed movies that the onset of the reaction indeed is amazingly fast. The transition from seemingly no reaction to explosive violence can occur in less than a few tens of ms, while the induction time can be tens of seconds or even minutes. The sequence below shows 12 frames of the start of a reaction, which occurred approximately 30 seconds after adding solid sodium bromate to a solution of hydroxyl ammonium chloride. The time between two frames is 5 ms.

In this webpage, a theoretical explanation is given of the mechanism behind the peculiar and very special dynamics of this reaction. A dynamical model is derived of this reaction and by means of simulations it is shown that the model captures behavior of the real system quite well. A set of differential equations for the concentration of a few chemicals is determined and this set is solved numerically. By playing with parameters of the model and by modifying the initial concentrations of the reactants, the model is tested and it is compared with the behavior of the real system.

Required chemicals:

• sodium bromate
• potassium bromide (or sodium bromide)
• hydroxyl ammonium chloride
• dilute sulphuric acid

Required equipment:

• test tubes

Safety:

• Sodium bromate is a strong oxidizer.
• Sodium bromate is a suspected human carcinogen. Do not eat or drink anything when working with this chemical in order to avoid intake of bromate ion.
• Hydroxyl ammonium chloride is toxic. Avoid exposure to this chemical.
• Dilute sulphuric acid is corrosive.
• Never mix larger amounts of bromate and hydroxyl ammonium salts. Do not scale up the experiments, described in this webpage. Even quantities as low as a few hundreds of mg may lead to very violent explosions.

Disposal:

• The liquid waste, produced in this experiment, can be flushed down then drain with a lot of water.

Procedure for performing the experiment: chemicals in solution

Take approximately 200 mg of hydroxyl ammonium chloride and dissolve this in as little as possible of cold water. This can best be done by taking a dry test tube, add the solid chemical and then add water drop by drop and swirl, until all of the solid has dissolved.

Take approximately 200 mg of sodium bromate and dissolve this in a little warm water. Do this in a dry test tube and then add approximately half a ml of water and carefully heat, until all of the solid has dissolved. No strong heating is needed, probably less than 50 ºC.

Pour the solution of sodium bromate in the solution of hydroxyl ammonium chloride and swirl the test tube for two or three seconds to mix the liquids. Then put the test tube aside and step back and wait. Do not look into the test tube from above and never point the test tube towards people.

After a few tens of seconds, a VERY violent reaction starts. A loud POP sound, or a very strong HISSSS is heard and after that, the liquid in the test tube appears to be gone. Most of the liquid is ejected from the test tube as vapor! A slow motion video (recorded at 100 frames per second, playback at 25 frames per second) shows how amazingly fast this reaction is and how long it takes, before the reaction starts: Video of slow motion (4 times) liquid/liquid mix. Download size is approximately 10 MByte. Below, a sequence is shown of how the reaction proceeds through the liquid. Time between frames is 10 ms.

Procedure for performing the experiment: solid sodium bromate

Take approximately 100 mg of hydroxyl ammonium chloride and dissolve this in as little as possible of cold water. This can best be done by taking a dry test tube, add the solid chemical and then add water drop by drop and swirl, until all of the solid has dissolved.

Take approximately 100 mg of sodium bromate and add this solid to the solution of hydroxyl ammonium chloride. Put the test tube aside and step back and wait. Do not look into the test tube from above and never point the test tube towards people.

With this experiment there is some room for playing around with amounts of the chemicals used. Both chemicals can be used in amounts from 50 mg to 200 mg. You can use excess amounts of sodium bromate or excess amounts of hydroxyl ammonium chloride. In all experiments, use just enough water to dissolve the hydroxyl ammonium chloride and add the solid sodium bromate.

A minute after adding the solid sodium bromate, a loud POP sound can be heard, and some fizzling occurs after the reaction, because not all of the sodium bromate will have reacted after the initial POP. A few videos were made of the reaction of solid sodium bromate with a solution of hydroxyl ammonium sulfate:

• Excess amount of sodium bromate, real time (download size appr. 2.5 MByte).
• Excess amount of hydroxyl ammonium chloride, real time (download size appr. 1.5 MByte).
• Slow motion video, 8 times as slow as real time (download size appr. 10 MByte).
• Demonstration of impressive sound of reaction, real time (download size appr. 8 MByte).

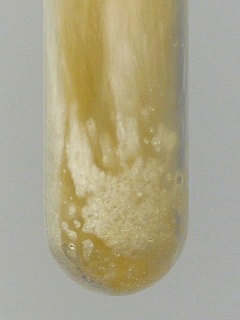
Below, a particularly violent sequence is shown. In this video, nearly 250 mg of sodium bromate was used in a luke-warm concentrated solution of hydroxyl ammonium chloride. After an induction period of half a minute or so, there was a loud PANG, followed by a spray of droplets, ejected from the test tube. Time between two frames is just 5 ms, so the explosion occurs in only 5 ms!

Effect of initially adding some bromide or some acid

The experiments, as described above can be slightly modified. One option is to add some bromide to the solution of hydroxyl ammonium chloride before adding the sodium bromate. When this is done, then the outcome of the experiment is quite similar, but the induction period is shorter. The more bromide is added, the shorter the induction period. The final effect, however, is quite similar. After the induction period there is a very violent, nearly explosive reaction.

Adding some acid before adding the sodium bromate leads to quite different behavior. The reaction then starts immediately after adding the sodium bromate, but not nearly as violent. The reaction starts with bubbling and in a few seconds the bubbling becomes very violent, but not explosive. It is more like a classical runaway reaction.

When both some acid and some bromide are added to the hydroxyl ammonium chloride, before adding sodium bromate, then the very violent reaction sets off immediately. There is no induction period at all. The reaction, however, is not explosive in this case.

Net reactions of bromate and hydroxyl ammonium ion

The reaction, demonstrated in this experiment, is not a simple one. It is possible to write down a main net reaction and a side reaction. The main reaction is as follows:

    (1)    6NH₃OH⁺ + 2BrO₃^– → 3N₂O + 2Br ^– + 6H⁺ + 9H₂O

There also is a side reaction, but the amount of nitrous acid only is a small fraction of the amount of N₂O:

    (2)    3NH₃OH⁺ + 2BrO₃^– → 3HNO₂ + 2Br ^– + 3H⁺ + 3H₂O

In a subsequent reaction, especially at elevated temperature, part of the nitrous acid decomposes to water, NO and NO₂. This leads to a pale brown color of the air in the test tube.

Reaction mechanism

The above reaction equations of course do not represent the real mechanism of the reaction, these are only net effects of the oxidation. The true reaction mechanism is very complicated and most likely still not completely known. There are many steps involved, but only a few steps are so slow that their description requires a differential equation. Other steps are either equilibria, or subsequent reactions, which occur at very high speed. Equlibria lead to algebraic constraints in the rate equations, very fast subsequent reactions can be summarized in net equations to final products and can be used to eliminate concentrations of intermediate species from the rate equations.

One (fairly slow) reaction path is the transfer of an oxygen atom from bromic acid ion (in equilibrium with bromate ion) to an hydroxyl ammonium ion:

     (3)    BrO₃^– + H⁺ + NH₃OH⁺ ↔ HBrO₃ + NH₃OH⁺ → HBrO₂ + NH₂(OH)₂⁺

The species NH₂(OH)₂⁺ is a transient species and this quickly decomposes to N₂O, H⁺ and water:

    (4)    NH₂(OH)₂⁺ → ½N₂O + 1½H₂O + H⁺

This decomposition reaction (4) is very fast, compared to the reaction between BrO₃^–, NH₃OH⁺, and H⁺.

N₂O is not further oxidized, this is quite inert. A small fraction of the species NH₂(OH)₂⁺ is oxidized further, before it has a chance to decompose,  to NH(OH)₃⁺, which immediately decomposes to HNO₂, H⁺ and water.

The part of hydroxyl ammonium ion, which makes it to HNO₂ only is a small fraction of the total amount, it is at most a few percent. Despite this low percentage, the effect of formation of HNO2 is clearly visible, due to its decomposition and subsequent formation of NO and NO₂. The brown color of NO₂ is clearly visible in some of the experiments. For the derivation of a model, which can explain the observed behavior, however, the side reaction, leading to formation of nitrous acid is not taken into account. It does not affect the global behavior of the dynamics of the model.

The species HBrO₂ is very reactive and very quickly reacts with hydroxyl ammonium ion in a chain of subsequent reactions, which finally leads to formation of bromide and N₂O. The net reaction is as follows:

     (5)    HBrO₂ + 2NH₃OH⁺ → N₂O + Br ^– + 3H⁺ + 3H₂O

Reaction (5) in reality is a chain of reactions, but the entire chain is very fast. In practice it can be considered immediate.

The rate at which reaction (3) occurs is a function of [BrO₃^–], [NH₃OH⁺], and [H⁺]. The species NH₂(OH)₂⁺ and HBrO₂ are intermediate and very short lived.

Once some bromide is formed in the system, another reaction kicks in. This reaction becomes much faster than reaction (3), once a decent amount of bromide ion has formed:

     (6)   BrO₃^– + Br ^– + 2H⁺ → HBrO + HBrO₂

At low concentration of bromide ion, this reaction is slow. So, only in a later stage, when quite some bromide is present in the system, this reaction really kicks in and causes positive feedback in the system, causing the system to 'explode'.

The species HBrO and HBrO₂ are very reactive. In a chain of reactions they react with hydroxyl ammonium ion with final products being bromide and N₂O. See reaction (5) above, and the following reaction:

     (7)    HBrO + NH₃OH⁺ → ½N₂O + Br ^– + 2H⁺ + 1½H₂O

At the same time, they also react with bromide and acid ions, to form bromine and water. These reactions also are very fast.

     (8)    HBrO₂ + 3Br ^– + 3H⁺ → 2Br₂ + 2H₂O

     (9)    HBrO + Br ^– + H⁺ → Br₂ + H₂O

The part of HBrO and HBrO₂ which goes into reactions (5) and (7) depends on the concentration of hydroxyl ammonium ion, relative to the concentration of bromide ion.

Once some bromine is formed in the system, another third reaction kicks in. The bromine oxidizes hydroxyl ammonium ion through a number of intermediate steps, which are not yet fully known. The net reaction is studied carefully, however, and is known to be first order in the concentration of bromine and the concentration of hydroxyl ammonium ion. The net reaction equation is

     (10)    Br₂ + NH₃OH⁺ → ½N₂O + 2Br ^– + 3H⁺ + ½H₂O

This reaction goes fast and as long as there is a decent concentration of hydroxyl ammonium ion in the system, the bromine is captured as soon as it is formed. The reaction, however, cannot be considered instantaneous, that would be too much of a simplification for determining a good model of the system.

Derivation of the rate models

Three reactions cannot be considered instantaneous, they need to be described by means of rate equations. In this section, the reaction rate is presented for all three of these reactions. These reaction rates are not determined experimentally in this web page, they are based on previous work, described in a few papers.

The dynamics of reaction (6) are well-known already for quite a few years and there even are simple student practice labs, which demonstrate these dynamics. A nice example of such a lab is given here. The reaction rate is written as k_Br·[Br ^–]·[BrO₃^–]·[H⁺]², where k_Br is some rate constant, which is determined experimentally. At high concentrations of bromide ion (in the order of magnitude of 1 mol/l), this rate equation does not hold fully, a better approximation (better by approximately 30%) is to add a quadratic term as well in the concentration of bromide ion:

     r₁ = k_Br·[Br ^–]·[BrO₃^–]·[H⁺]² + k_Brs·[Br ^–]²·[BrO₃^–]·[H⁺]²

For most models it probably is sufficient to ignore the second term, but adding this term is only a little effort and a good estimate of the parameter k_Brs is available from a published paper, it is determined experimentally. Simulation results, however, show little effect of adding this term, the qualitative behavior of the model hardly is affected by this term.

The rate at which bromate ion is consumed, due to reaction (6) equals r₁.

The reaction rate for reaction (3) between bromate and hydroxyl ammonium ion is studied as well. The rate is derived in this paper. The rate is first order in the concentration of bromate ion and hydroxyl ammonium ion, but it is more complicated in the concentration of acid ion H⁺. Bromate ion is in equilibrium with bromic acid and hydroxylamine is in equilibrium with hydroxyl ammonium ion. It is the species HBrO₃ which reacts and hence the appearance of the K_z constants of the acids HBrO₃ and NH₃OH⁺. According to the paper, the reaction rate is as follows:

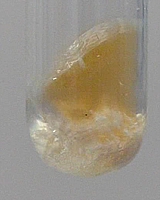
     r₂ = k_N·[NH₃OH⁺]·[BrO₃^–]·{H⁺}, where {H⁺} equals K₁·[H⁺] / (1+K₁·[H⁺])K₂

Here, K₁ is 1/K_z of bromic acid, K₂ is 1/K_z of hydroxyl ammonium ion. According to literature (published tables of K_z values of many acids), the numerical values are approximately 5.0 and 1.0·10⁶. The paper uses the wrong value 0.5 for K₁, but it correctly describes this constant as the reciprocal value of the acid constant of bromic acid.

The value k_N is a rate constant, which is determined experimentally.

The rate at which bromate ion is consumed, due to reaction (3) equals r₂.

The same paper briefly touches upon the reaction between bromine and hydroxyl ammonium ion. It does not give a description of the reaction mechanism, it only describes the net reaction rate.

     r₃ = k_Br2·[NH₃OH⁺]·[Br₂]

The constant k_Br2 is determined experimentally and published in the above mentioned paper.

The rate at which bromine is consumed, due to reaction (10) equals r₃.

Derivation of the differential equations, based on rates and reaction stoichiometry

There are only 5 species, which really need to be described in the differential equations. All other species are very short lived and immediately are converted to one of the 5 longer lived species. Five state variables x₁, x₂, ..., x₅ are introduced as follows:

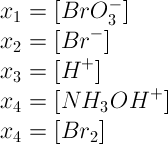
Using these state variables, the rates can be expressed as follows:

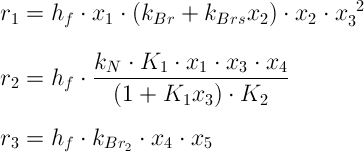
An additional factor h_f is introduced, this is explained further below.

The time derivative of all state variables now can be written as functions of r₁, r₂, and r₃.

Deriving the differential equations for the states x₁, x₂, ..., x₅ can be done on the basis of equations (3), (6) and (10). There is one uncertainty in the model and that is that the intermediate species HBrO and HBrO₂ partially react with bromide to form bromine and partially with hydroxyl ammonium ion to form mainly N₂O and bromide. In this model, a constant α is introduced and it is said that part α of HBrO and HBrO₂ reacts with bromide to form bromine and part 1–α of HBrO and HBrO₂ reacts with hydroxyl ammonium ion to form N₂O and bromide. This strategy works well. In fact, the precise choice of α does not matter at all. The result of the simulations is independent of α! This is because the subsequent reactions are very fast and it does not matter what exact route is followed in the course of these final reactions. The system in any case ends up with bromine if there is excess bromate and the system ends up with bromide (either through intermediate bromine, or directly from HBrO and HBrO₂), but the stoichiometry of course is not different for these paths. In reality one can safely assume that both paths will be followed concurrently, but the final net effect is the same. So, in the simulation, the parameter α is wisely eliminated by taking it equal to [Br ^–]/([Br ^–]+[NH₃OH⁺]). The value of 1–α equals [NH₃OH⁺]/([Br ^–]+[NH₃OH⁺]).

Derivation of the differential equations now is an easy but tedious job. It is a matter of careful bookkeeping of consumption and production of compounds and all concentrations of short lived intermediate species must be expressed in concentrations, corresponding to the state equations.

From equations (3), (4), (5), and (8) follows the following equation (3'), where replacement of the intermediate species NH₂(OH)₂⁺ and HBrO₂ is marked by color. The further reaction of intermediate species HBrO₂ leads to extra consumption of bromide ions, acid ions and hydroxyl ammonium ions. These are put at the left with correct factors α and (1-α). The products are put at the right.

     (3)    BrO₃^– + H⁺ + NH₃OH⁺ → HBrO₂ + NH₂(OH)₂⁺

     (3')   BrO₃^– + 3αBr ^– + 3αH⁺ + 2(1-α)NH₃OH⁺ + H⁺ + NH₃OH⁺ →

                          2αBr₂ + 2αH₂O + (1-α)N₂O + (1-α)Br ^– + 3(1-α)H⁺ + 3(1-α)H₂O +  ½N₂O + 1½H₂O + H⁺

Now, for each of the states x₁, x₂, ..., x₅ the contribution of rate law r₂ can be determined.

       dx₁/dt = –r₂ + <contributions from r₁ and r₃>

       dx₂/dt = –3αr₂ + (1-α)r₂ + <contributions from r₁ and r₃>

       dx₃/dt = –r₂ – 3αr₂ + 3(1-α)r₂ + r₂ + <contributions from r₁ and r₃>

       dx₄/dt = –r₂ – 2(1-α)r₂ + <contributions from r₁ and r₃>

       dx₅/dt = 2αr₂ + <contributions from r₁ and r₃>

A similar thing can be done for equation (6) with rate law r₁. This adds terms to the expressions, shown above. Finally, the same can be done for equation (10) with rate law r₃. This leads to the following final set of equations:

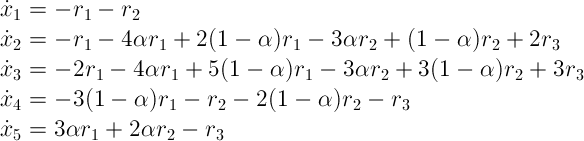
This entire set can be simulated, using a suitable numerical integration method. A Java program was written to simulate this set. It uses a robust modified Runge-Kutta method. This model has parameters in its rate laws. These parameters were determined experimentally (see papers, mentioned above):

      k_Br = 2.025

      k_Brs = 0.7

      k_N = 2.57·10³

      k_Br2 = 1.7·10³

Besides these four experimentally determined parameters, the model has two reciprocals of Kz-constants for bromic acid and hydroxyl ammonium ion. These are K₁ = 5.0 and K₂ = 1.0·10⁶. One more artificial parameter is added, being h_f. This is not a constant, but it is used to model the effect of heating up of the liquid. This effect is hard to model accurately, so it only can be used to get a qualitative idea of its influence. The model takes into account the amount of bromate ion, used up in the reaction and assumes no loss of heat during the reaction. This is a valid approach in the test tube experiments where a transition occurs from hardly any reaction to near explosion in a fraction of a second. Assuming a doubling of reaction rate for every 10 ºC and assuming heating up of appr. 70 ºC when all bromate is used up, the following value can be used for h_f:

      h_f = 2^7·([BrO3^ˉ]0 ^{– [BrO}3^ˉ])

This probably is a conservative estimate of the effect. In reality it might well be stronger (e.g. in some of the experiments it is observed that the solution escapes as a plume of steam from the test tube).

The used Runge-Kutta method sometimes had a hard time to solve the set of equations. Simulation was done in steps of 0.01 second with an initial integration stepsize of 0.001 second, but when the parameter h_f is chosen less conservative (e.g. 3 to the power ... instead of 2 to the power ...), then a much smaller initial integration step size must be chosen and then the simulation takes a long time!

Simulation results of the model

The model captures the behavior of the real system quite well. When it is simulated with an initial concentration of 1 mol/l for the bromate ion and an initial concentration of 2 to 4 mol/l of the hydroxyl ammonium ion, then it shows a very sharp transition, several tens of seconds (appr. 1 minute) after the start of the reaction. Below follow some graphs with simulation results, using different starting concentrations. The horizontal axis is time in seconds, the vertical axis is concentration in mol/l. All simulation results, displayed below, and the Java source code are available in a zip file.

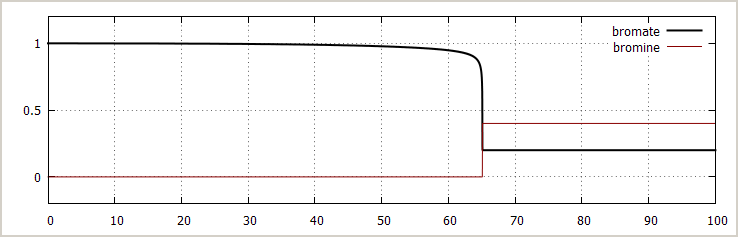
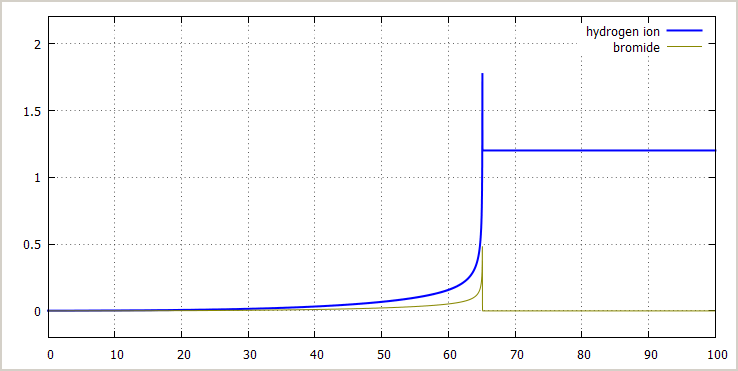
Excess bromate ion, no initial bromide or acid added: The pictures below show the concentration of bromate ion, bromine, hydrogen ion and bromide ion as function of time, with initial concentrations as follows:

     [BrO₃^–]₀ = 1 mol/l

     [NH₃OH⁺]₀ = 2 mol/l

    [H⁺]₀ = 1.4·10^-3 mol/l (no added acid, this small concentration is from equilibrium of NH₃OH⁺)

     [Br ^–]₀ = 0 mol/l

     [Br₂]₀ = 0 mol/l

Here you can see a sharp transition. The bromine concentration goes from nearly 0 to 0.4 mol/l in just 0.03 seconds. Similar sharp transitions occur in the concentration of other compounds. The concentration of hydroxyl ammonium ion is not plotted, but it follows the curve of the concentration of bromate, except that it starts at 2 and ends at 0.

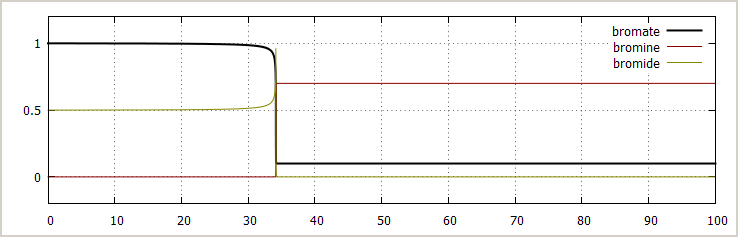
Excess bromate ion, some initial bromide added: The picture below shows the effect of adding some bromide initially:

     [BrO₃^–]₀ = 1 mol/l

     [NH₃OH⁺]₀ = 2 mol/l

    [H⁺]₀ = 1.4·10^-3 mol/l (no added acid, this small concentration is from equilibrium of NH₃OH⁺)

→ [Br ^–]₀ = 0.5 mol/l

     [Br₂]₀ = 0 mol/l

The qualitative behavior is similar, but the sharp transition occurs earlier. This is confirmed with experiments.

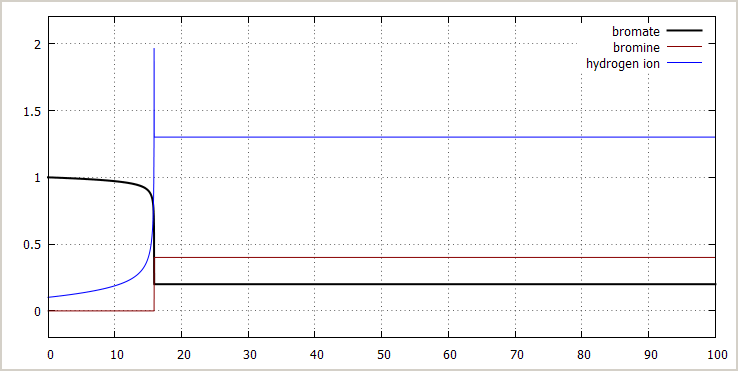
Excess bromate ion, some initial acid added: The picture below shows the effect of adding some acid initially:

     [BrO₃^–]₀ = 1 mol/l

     [NH₃OH⁺]₀ = 2 mol/l

→ [H⁺]₀ = 0.1 mol/l

     [Br ^–]₀ = 0.0 mol/l

     [Br₂]₀ = 0 mol/l

The effect of adding acid is stronger than the effect of adding bromide ion. Even addition of a small amount of acid (e.g. 0.1 mol/l) makes occurrence of the transition much earlier.

When bromide ion and acid are added both, then there hardly is any delay. The simulation then shows immediate reaction, which in a few seconds becomes very violent. This also happens in a real experiment.

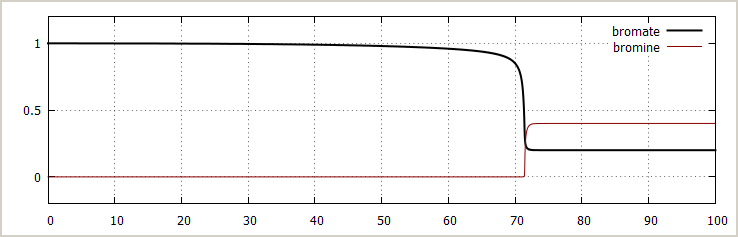
Excess bromate ion, perfect removal of heat: In this simulation the heating effect is removed from the model. In reality this experiment could not be done, but it is interesting to see whether the explosion is due to heat or due to the properties of the reaction mechanism itself. The answer is that it is the combination of both effects which causes the explosive violence. Heating up alone only would lead to a runaway, and the dynamics of the reaction alone would lead to an induction time, but the transition would not nearly be as violent as the one observed in the real experiment.

     [BrO₃^–]₀ = 1 mol/l

     [NH₃OH⁺]₀ = 2 mol/l

    [H⁺]₀ = 1.4·10^-3 mol/l (no added acid, this small concentration is from equilibrium of NH₃OH⁺)

     [Br ^–]₀ = 0.0 mol/l

     [Br₂]₀ = 0 mol/l

Here you can see that the concentration of the bromate ion and the concentration of bromine are still steep functions of time during the transition, but there is a clearly visible slope now, the lines are not vertical.

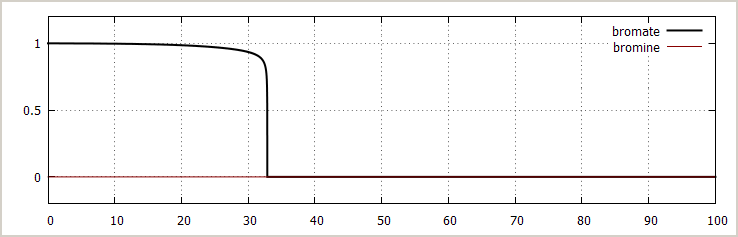
Excess hydroxyl ammonium ion: The effect of adding more hydroxyl ammonium ion initially is not very strong. The transition occurs earlier, just as expected, and at the end of the reaction, no bromate ion remains and all bromate is converted to bromide ion.

     [BrO₃^–]₀ = 1 mol/l

→ [NH₃OH⁺]₀ = 4 mol/l

    [H⁺]₀ = 2.0·10^-3 mol/l (no added acid, this small concentration is from equilibrium of NH₃OH⁺)

     [Br ^–]₀ = 0.0 mol/l

     [Br₂]₀ = 0 mol/l

During the entire reaction, the amount of bromine remains nearly 0. Only during the very short time of the transition, the bromine concentration has a small peak in the order of magnitude of 0.001 mol/l, which lasts for less than 0.01 seconds. This is because the reaction of bromine with hydroxyl ammonium ion is very fast and as soon as it is formed, it is destroyed again.

Conclusions

The remarkable dynamics of the reaction between bromate ion and hydroxyl ammonium ion can nicely be explained by the model, described above. The model explains induction time, it also explains the effect of initially adding bromide ion or acid. It also shows that it is the combination of heating up and the strong transition due to reaction dynamics which leads to the spectacular observed behavior of the system.

back to top of page

back to main experiments page