Synthesis of potassium metaperiodate, KIO₄

Periodates are hard to obtain for the home chemist, and they are very expensive. These compounds are quite interesting and it is fairly easy to make them from iodates. Iodates are easier to obtain, and although these still are not the cheapest reagents, they usually are a lot cheaper than periodates.

This page describes how potassium (meta)periodate can be made from potassium iodate, using very simple glassware and a small alcohol burner.

In this experiment a large amount of elemental chlorine is prepared, which normally does not escape into the air, but in case of an error there may be unintended release of this gas.

Required chemicals:

• potassium iodate

• potassium hydroxide

• trichloro cyanuric acid in the form of tablets (TCCA)

• hydrochloric acid (15%)

• nitric acid (15% to 20%, if not present, then one may use hydrochloric acid instead, but the yield probably is somewhat less)

Required equipment:

• alcohol burner

• beaker

• erlenmeyer

• stoppers and tubing (preferably glass, rubber or plastic also works, but after use it must be discarded)

Safety:

• Potassium hydroxide is very corrosive.
• TCCA is a strong oxidizer and corrosive.
• Potassium periodate is a strong oxidizer.
• A lot of chlorine gas is prepared in this experiment. In case of unintented release unto the air, assure that no chlorine gas is inhaled. This gas is very corrosive and poisonous.

Disposal:

• The liquid waste from this experiment is not particularly toxic. It may be flushed down the drain with a lot of water.
• The chlorine generator produces solid cyanuric acid, and it may be interesting to purify and isolate this as well. If one does not want or need this, then it can be filtered and discarded as solid household waste.

The starting chemicals

The starting chemicals are potassium iodate and potassium hydroxide, dissolved in water, through which chlorine gas is bubbled. The pleasant property of this synthesis is that the amounts of chemicals are not critical at all, the synthesis is very forgiving for inaccurate measurements. A "recipe" for this experiment is as follows:

• take 5 grams of KIO₃
• take 6 grams of KOH
• dissolve in water and keep boiling
• pass chlorine through the solution, until no more chlorine is absorbed.

With these quantities of chemicals, the yield of potassium periodate, KIO₄, can be over 5 grams. Below, a report of a practical run is given.

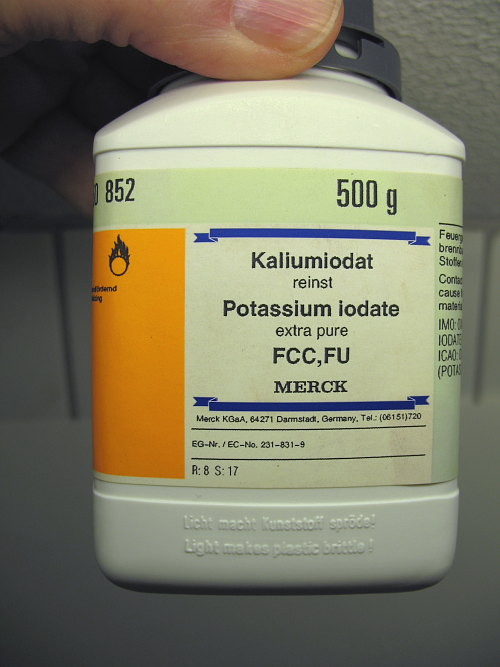
Roughly 5 grams of potassium iodate were taken. More precise measurement showed that 5.6 grams were used. For the potassium iodate, high quality material was used:

To this, 6.8 gram of potassium hydroxide was added. The purity of the potassium hydroxide is somewhat uncertain, it can be as low as 90%, due to the presence of water and small amounts of potassium carbonate.

This picture shows the potassium iodate and the potassium hydroxide, added to each other in a beaker.

The amount of chlorine is not determined in advance. Roughly 5 gram of TCCA was taken, in the form of coarse chunks (average chunk diameter 1 cm or so), irregular shape, made by carefully hitting a tablet with a hammer. Three of these chunks were put in an erlenmeyer and 20 ml of 15% hydrochloric acid was added). During the experiment additional chunks were added if chlorine production became too slow.

The setup of the apparatus

The apparatus was setup with an intermediate test tube, through which the chlorine gas is passed. The test tube was simply a dry test tube without any material. Its only purpose is to assure that no suckback can occur, nor that foam from the chlorine generator can flow into the beaker with the potassium periodate. The picture below shows a schematic drawing of the setup.

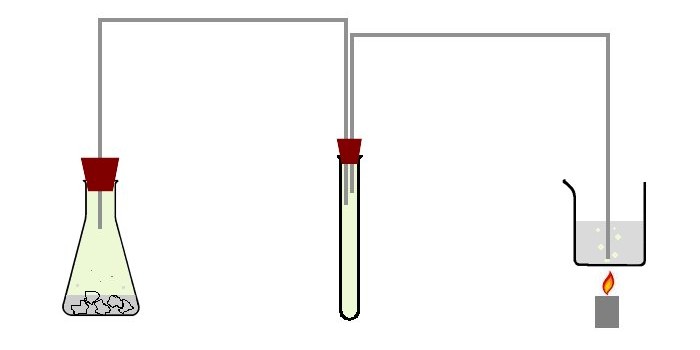
At the left there is a chlorine generator, which simply is a 100 ml erlenmeyer with some hydrochloric acid and chunks of TCCA in it. It is stoppered with a rubber stopper, which has one hole. A thin tube is going to the test tube in the middle. The test tube in the middle is stoppered with a rubber stopper, which has two holes. A second thin tube is going to the beaker with the potassium iodate/potassium hydroxide solution. The beaker is heated above a small flame, such that the solution remains near boiling.

The practical setup is shown in the following picture (now the chlorine generator is at the right and the beaker with solution is at the left).

The thin tube is made from thin glass tube and melted and bent in the right shape. These glass tubes can be reused, while plastic tubing degrades very quickly when chlorine gas is passed through it. If no such glass tubing is available, then one can use thin plastic tubing for an aquarium tank, but this must be discarded at the end of the experiment.

Putting the setup in action

The beaker with potassium iodate and potassium hydroxide is filled with 50 ml of water and put above the flame. Small amounts of water are added, each time when the liquid boils and still some solid remains. In this particular run, 80 ml of solution was obtained, before all potassium iodate dissolved. It is very important that all potassium iodate dissolves. When all of the potassium iodate finally has dissolved, then add 3 ml more of water, to keep a little headroom for evaporation of the liquid. Total amount of solution with 5.6 grams of potassium iodate and 6.8 grams of potassium hydroxide was between 80 and 85 ml.

As soon as all solid material has dissolved, fill the erlenmeyer with 20 ml of 15% hydrochloric acid and throw in 3 chunks of TCCA. Chlorine production starts at once, a nice continuous fairly fast stream of chlorine is produced, but it never becomes violent. Initially, the bubbling in the beaker is fast (too fast, a small amount of the liquid bumped over the rim of the beaker), but once the entire gas generator, test tube and thin glass tubing is filled with chlorine, the bubbling becomes much more relaxed. Really all chlorine dissolves in the solution, even when one sticks the nose just a few cm above the beaker, no chlorine can be smelled. The initial violent bubbling is because of the air, which does not dissolve. So, it is suggested to first let the gas generator flow for a few seconds and as soon as chlorine is coming out of the tubing, then it is immersed in the liquid and the open end of the tube is put near the bottom of the beaker.

The picture below shows the chlorine generator in action. The chlorine generator produces quite some foam, due to the insoluble cyanuric acid, formed in the reaction. Some of this foam even made it into the test tube, so indeed it was very good that there is a test tube inbetween, otherwise it would have spoilt the solution with the potassium iodate.

The picture below shows that the test tube has splashes of foam inside.

The chlorine gas nicely bubbles through the liquid, but the bubbles never make it to the surface, they very quickly dissolve in the alkaline liquid. The picture below nicely shows a bubble at the right of the beaker, near the bottom. The liquid is totally clear, and while chlorine is bubbled in, it becomes a little yellow/green, while initially it is colorless.

A video is made from the bubbling as well (not the best video, it was not made from a tripod, no space was left for that). The video, however, nicely shows the speed at which the chlorine bubbles are released into the liquid. Download size of the video is approximately 1 MByte.

Near the end of the reaction

While chlorine is bubbled into the liquid, it first becomes more and more green, but at a certain point, it becomes almost colorless again or very pale green. Near the end of the experiment, a fine crystalline precipitate is formed as well, and the liquid starts bumping due to the heating. If this bumping becomes too strong, then the alcohol burner may be removed, as this is almost the end of the experiment. The following animation shows the bumping of the liquid, the bubbles of chlorine hardly can be seen due to the bumping: bumping.avi.

As soon as the chlorine is not completely absorbed by the liquid anymore (smell!) then passing chlorine through the liquid must be stopped. At this point there is a fairly large amount of white crystalline precipitate and the liquid has become almost colorless again. Bubbles now make it to the surface and a strong smell of chlorine can be observed: bubbling2.avi.

When no more chlorine is passed through the liquid, then it quickly becomes colorless.

Working up the periodate

The still hot liquid contains quite some periodate in solution, only part of the periodate is present as a precipitate on the bottom. The periodate in solution also partly is present as the orthoperiodate, which dissolves in water much better than the metaperiodate (at least for the potassium salt, not for the sodium salt). In order to get all periodate from solution, the liquid must be slightly acidified, such that all orthoperiodate is converted to metaperiodate and the periodate precipitates as the potassium salt.

The addition of the acid must be done dropwise while stirring with a glass rod. While this is done, the liquid becomes darker green again and at a certain point small bubbles of chlorine are produced, and at that point one must stop adding more acid. Best is to use nitric acid, as this cannot be reduced by the periodate, but if no nitric acid is available, hydrochloric acid can also be used, but then one must be really careful not to add too much and one must use a concentration not more than 10%. With nitric acid, the addition of somewhat too much acid is not a problem.

Addition of the acid causes formation of more precipitate. Very fine crystals of potassium metaperiodate are formed slowly and these settle at the bottom quickly. The liquid looks as shown in the picture, it is light green, and a large amount of compact precipitate is at the bottom.

When a picture is made from above, then one can clearly see the slow bubbling of the chlorine gas. Altogether, only 1.5 ml of 15% nitric acid was added to the liquid, before this situation was obtained.

After stirring, the precipitate is spread nicely over the bottom, the picture shows that a fairly thick layer of precipitate is present.

Purification of the crystalline solid is fairly easy. The precipitate is really compact and the liquid above it can be decanted. Let the liquid cool down and then decant the liquid from the compact crystal mass. Do not yet filter, only decant! The chlorine in the liquid attacks the filter paper too much and this introduces impurities. When the liquid is decanted, add 20 ml of cold distilled water and swirl well. Let the precipitate settle again and decant the liquid as well as possible without loosing solid material. Repeat this another two times. Mechanical losses, due to the decanting are minimal and losses due to dissolving also are minimal.

Next, put the wet crystal mass on a piece of filter paper, which in turn is put on top of a few sheets of soft paper tissue. The filter and paper tissue nicely absorb the adhering liquid from the crystal mass and a compact rather dry mass is obtained already. Any impurities in the adhering liquid now also go into the paper tissue, making the solid more pure.

Scrape the mass from the filter paper onto a clean petri dish and spread a little bit.

Allow the solid in the petri dish to dry in a warm place, e.g. on a warm radiator at a temperature of 50 ēC or so. After one day, the solid mass is perfectly dry. Faster drying is possible, when the solid mass is crunched a little bit halfway the drying process.

Final yield

The final yield in the petri dish, after good drying, was 5.14 grams. This is 85% of theoretical yield and is quite good. Some material was sticking to the filter paper and also some material was left behind in the beaker, while transferring it to the filter paper. These mechanical losses are the greatest source of losses and they will become lower, when larger batches are used.

The underlying principle of this synthesis

The reaction for this synthesis is the following:

   IO₃^– + 4OH^– + Cl₂ → H₂IO₆^3– + 2Cl^– + H₂O

Iodate is oxidized to orthoperiodate by the chlorine. This reaction requires a high temperature, otherwise it runs slowly and there will be a lot of side reaction, in which chlorine disproportionates to chloride and chlorate in the alkaline solution.

The potassium salt of orthoperiodate, K₃H₂IO₆, dissolves in water fairly well, and there also is an equilibrium in water:

    H₂IO₆^3– ↔ IO₄^– + 2OH^–

When more chlorine is passed through the solution, then the hydroxide, formed in this reaction, is used up in the reaction, given above, and also in a disproportionation to chloride and chlorate (or hypochlorite). This leads to formation of metaperiodate in solution, which precipitates with the potassium ions, present in solution.

At the end, when not all chlorine is absorbed anymore, the solution still contains quite some orthoperiodate ions in solution. The addition of acid also converts this to metaperiodate:

    H₂IO₆^3– + 2H⁺ → IO₄^– + 2H₂O

This metaperiodate also precipitates with the potassium ions, present in solution. The precipitation is nearly quantitative, because KIO₄ is only very sparingly soluble in water, approximately 0.5 gram per 100 ml. In the presence of additional K⁺ ions, the solubility is even lower.

The practical synthesis is not critical at all, as long as there is sufficient potassium hydroxide in solution. A little bit too much is not a problem, it just leads to some chloride, chlorate and hypochlorite in the solution and hardly affects the yield.

Remark: A similar synthesis is possible with NaIO₃ and NaOH. In that case, the NaOH and NaIO₃ must be dissolved in water, and chlorine must be passed through. In this case, again an excess amount of NaOH must be used, in order to assure that all periodate precipitates. With the sodium salt, one should not acidify at the end. With the sodium salt, it is the orthoperiodate which is sparingly soluble and the metaperiodate dissolves quite well. So, while chlorine is bubbled through the solution a fine crystalline precipitate of Na₃H₂IO₆ is formed. In order to get really all periodate, some extra NaOH should be added after passing the chlorine through the solution.

Remark 2: If one only has KIO₃ and NaOH, then still one can produce periodate, but the resulting product will have a somewhat unsure composition. It will be a mix of metaperiodate and orthoperiodate, because metaperiodate precipitates with potassium ions and orthoperiodate precipitates with sodium ions. Addition of acid at the end will mainly make potassium metaperiodate and addition of sodium hydroxide will mainly make sodium orthoperiodate, but one never gets a pure potassium or pure sodium salt. Recrystallization from either weakly acidic or weakly alkaline solution is necessary to separate the sodium and potassium salts. For many practical purposes, however, such impurities are not a problem at all.

back to top of page

back to main experiments page