Chemical equation solver - getting started

In this page, a short introduction to chemeq.exe is given, such that you can use the program quickly without a steep learning curve. Just follow the examples.

Basics: balancing an equation

The primary goal of the program is to balance equations. This can be done very easily. In order to show how to do this, a somewhat less trivial example is given: the oxidation of sulphur dioxide by dichromate in acidic media, giving trivalent chromium ions and sulfate ion. This is a common redox reaction, often encountered in high-school chemistry textbooks.

The unbalanced equation for this is:

    Cr₂O₇^2- + SO₂ + H⁺  →  Cr³⁺ + SO₄^2- + H₂O

In order to balance this equation, we simply type the reactants and products in chemeq.exe, each reactant and product in a single box. Ionic charges are given between parentheses.

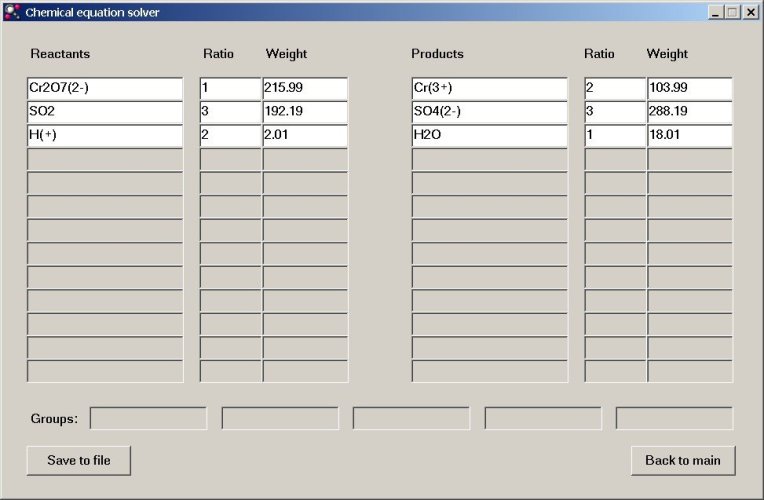
Next, click the "Solve equation" button and when this is done, a new window appears, with the coefficients in the ratio-columns and the total molecular weight in the weight column. So, the equation is balanced and the correct equation becomes:

    Cr₂O₇^2- + 3SO₂ + 2H⁺  →  2Cr³⁺ + 3SO₄^2- + H₂O

Basics: use as very simple molecular weight calculator

Sometimes one just wants the molecular weight of a single compound. Chemeq can also be used for such computations. One simply types the formula of the compound in one of the reactants boxes and then the "Solve equation" is clicked. Only one box may be filled with a formula, as soon as more boxes are filled, then the program does not work in this special mode anymore.

When the "Solve equation" button is clicked, then a new window appears, with the total molecular weight of the compound in the reactants weight column. The weight of each element in the compound is displayed in the product weight column.

In this mode, the program actually solves the equation, where the compound is completely decomposed into its elements.

In this simple mode, the program also supports the use of the groups boxes at the bottom of the window (see further below in this tutorial for how these can be used), so one may use special isotope elements, or groups of elements, which should not be broken down.

Basics: determining half reactions for redox reactions

A very common thing, needed for determining how redox reactions proceed, are the so-called half-reactions. There frequently are tabulated, together with a redox potential. Many people try to memorize these kinds of reactions, but chemeq.exe is capable of deriving them. What needs to be known is the input compounds or ions, the number of electrons consumed or produced, and the output compounds or ions. The computer program then determines the fully balanced half-reaction.

Some examples: dichromate, acting as oxidizer in acidic media, hence "consumption" of electrons.

Input: Cr₂O₇^2-, H⁺, e

Output: Cr³⁺, H₂O

This problem simply can be solved by typing Cr2O7(2-), H(+) and e in the reactants column and typing Cr(3+)and H2O in the products column. The result is as follows:

   Cr₂O₇^2- + 14H⁺ + 6e  →  2Cr³⁺ + 7H₂O

This is a well-known and frequently tabulated reaction. Things become more interesting when a much less common half-reaction needs to be derived.

As an example we use the half-reaction from the brown hypovanadate to colorless orthovanadate in strongly alkaline solutions. Hypovanadate contains vanadium metal in the +4 oxidation state and has formula V₄O₉^2- and orthovanadate contains vanadium in the +5 oxidation state and has formula VO₄^3-. The vanadium obtains a higher oxidation state and hence is reduced. It "produces" electrons. The reaction occurs in strongly alkaline environments, so we need hydroxide ion for compensation of oxygen. We do not know in advance whether the reaction consumes or produces hydroxide ion. We just try with water as input and hydroxide as output.

Input:  V₄O₉^2-, H₂O

Output: VO₄^3-, OH^–, e

The result of this is given by chemeq.exe as follows, when the "Solve equation" button is clicked:

   V₄O₉^2- – 7H₂O  →  4VO₄^3- – 14OH^– + 6e

Chemeq.exe shows that water and hydroxide has negative coefficients. These need to be reversed in order to get a correct equation:

   V₄O₉^2- + 14OH^–  →  4VO₄^3- + 7H₂O + 6e

In this way, chemeq.exe can be used easily to derive half-equations for reduction or oxidation.

Doing some automated computations

In this example we are studying the complete combustion of butane gas. The reaction products are water and carbon dioxide. The unbalanced equation for this is:

   C₄H₁₀ + O₂  →  CO₂ + H₂O

Again, we type the reactants and products, and we click the "Solve equation" button:

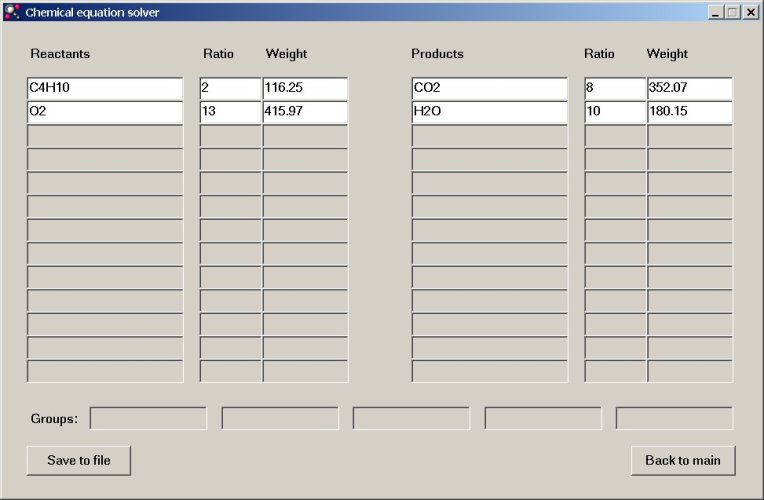
This gives the following result, which allows us to balance the equation:

   2C₄H₁₀ + 13O₂  →  8CO₂ + 10H₂O

The program, however, allows us to do more than simple balancing of equations. Suppose we are asked the question "How many grams of oxygen and how many mols of oxygen are needed for complete combustion of 10 grams of butane gas?". This question can very simply be solved. At the molecular weight field for butane edit the number 116.25 to 10. The other numeric fields (both ratio columns and weight columns) are adjusted accordingly, such that the overall stoichiometric ratios are still correct. So, one can edit the numeric fields. In the example below we are going to edit the weight field for butane (marked as red):

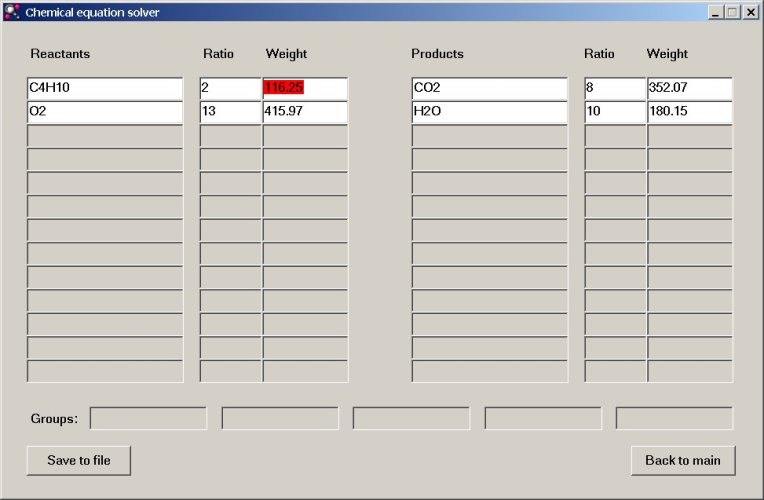
At this place we type the value 10:

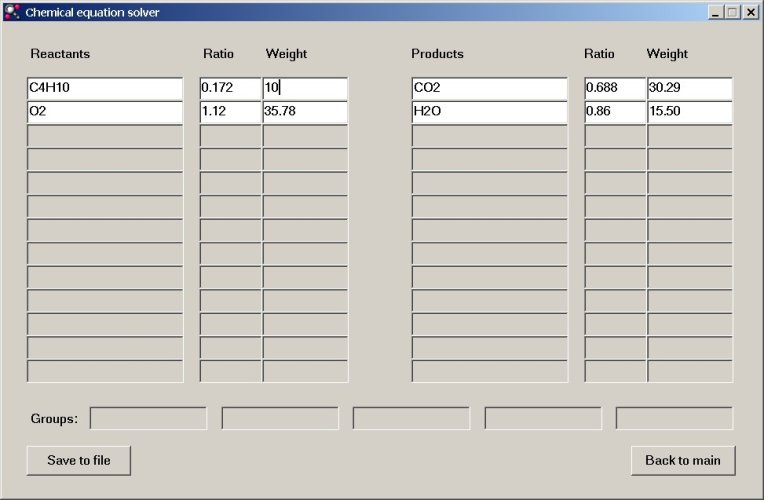
The other numeric values are adjusted within a fraction of a second. So, when 10 grams of butane are used, then 35.78 grams of oxygen are needed, which equals 1.12 mols of oxygen molecules O₂.

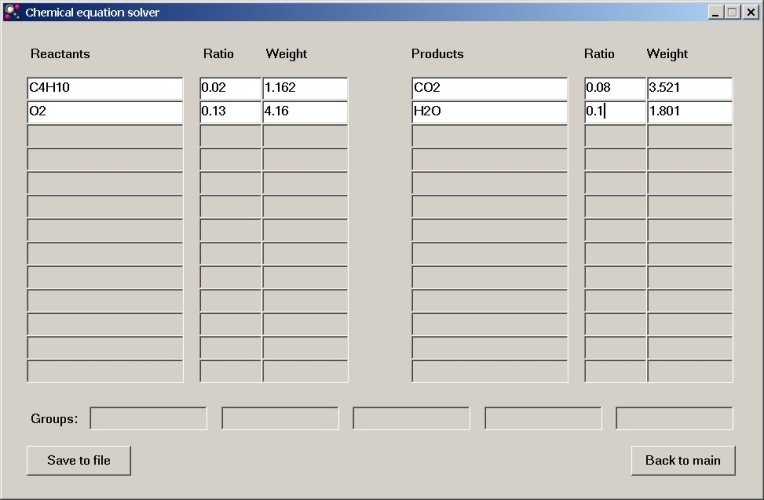
Now, suppose that we are asked the question: "How many grams of butane are needed to produce 0.1 mol of water?". In order to do so, we edit the "Ratio" box for water and type the value 0.1 and all other values are updated again. The answer to this question is 1.162 grams of butane.

What happens if garbage is typed in a numeric window? That is shown here, where the value "blurp" is typed for the number of mols of water. All other numeric boxes show ######.

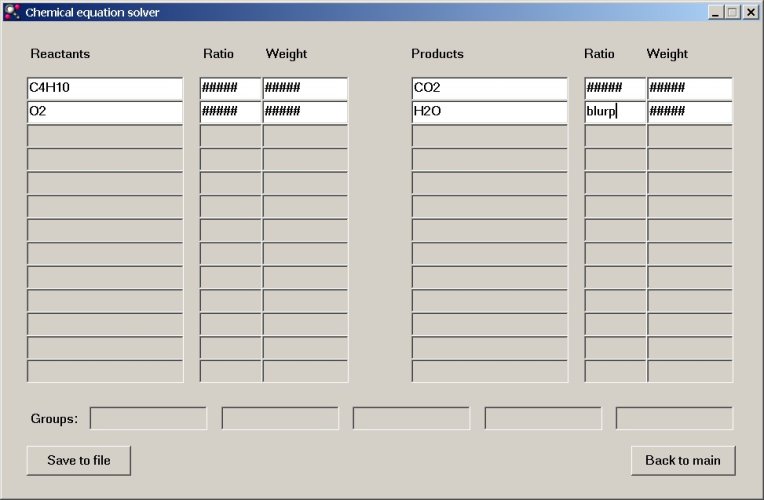
As soon as a correct numeric value is typed again, the other boxes display corresponding numeric values also again.

Using the numeric box values, one has great flexibility in computing ratios, both for weights and for number of mols of reactants and products. This feature of chemeq.exe has proven to be very useful and saves a lot of annoying and error-prone computations.

The use of isotopes or elements with special atomic weights

Up to now, no special elements have been used. Chemeq.exe, however, also supports working with isotopes or even virtual elements with any atomic mass. The balancing of equations is not different from what we have seen before, but this feature can be useful, when computations need to be made, such as shown in the example above with the combustion of butane. Suppose we have the same example, but instead of plain carbon, the butane is based on the special ¹⁴C isotope. Again, we want to perform the same kind of computations. In order to allow one to do such computations, one can define his own elements. This is done, using the "Groups" fields at the bottom of the window.

Now, we are going to study the combustion of C₃C'H₁₀, where C' is the ¹⁴C isotope of carbon. In the butane molecule, one atom is replaced by the ¹⁴C isotope. Using a lookup table, we find that the atomic mass of ¹⁴C equals 14.0032 grams per mol. We define a new element in one of the group fields. Which one is used does not matter. The element, defined in the group field can be used in the reactants and products fields, just as any other element.

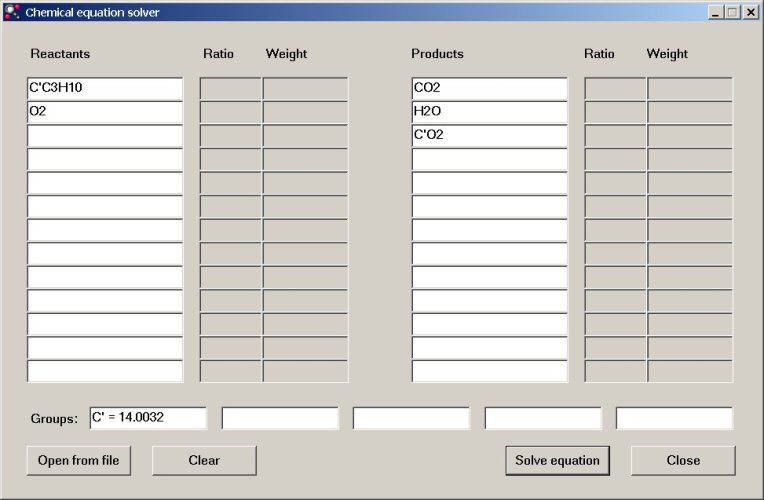
When a new isotope is added, then of course, the reactants and reaction products must also be changed accordingly. In the example with combustion of butane, two types of molecules of carbon dioxide will be formed, with the special isotope and with normal carbon.

If the "Solve equation" button is clicked, then the equation nicely is balanced, just as in the case with normal elements. The result is shown here.

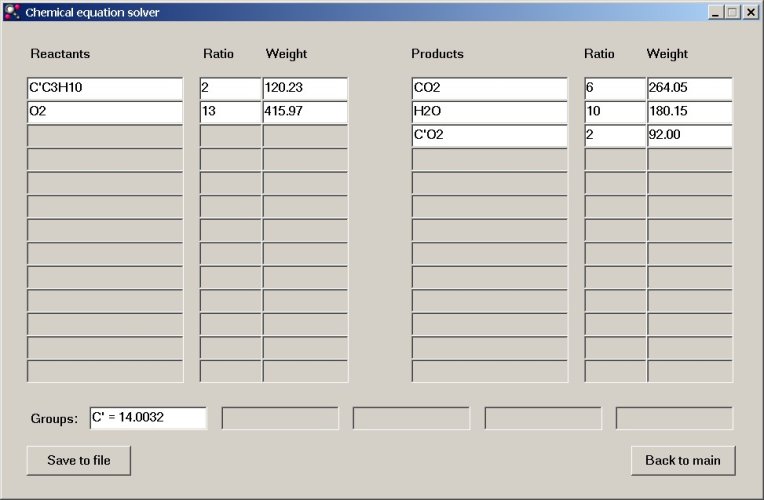
One also can edit the numerical fields just as in the previous example and all weights and ratios will be adjusted accordingly. Also look at the value for the weight of the butane and the carbon dioxide with the special isotope. It uses the value, entered in the "Groups" box.

One can introduce up to 5 new elements, this number being determined by the number of group boxes. The name of these new elements must start with a capital letter, and optionally two other characters can be added. These characters may be any lowercase letter, a ' or a *, digits are not allowed.

The following are valid names: Own, C', C'', Mmm, Mm, O*, Se*, O*', O'*, Lol, L*l.

The following are invalid: OWn, CC, C*L, LoL, C14, Se2.

Advanced issues: multidimensional solution spaces and grouping

Most chemical reactions can be covered quite well by the chemeq.exe program, if it had only the functionality, as described above. However, there also is a whole class of reactions, which cannot be balanced unambiguously. It is said that an equation can be balanced unambiguously, if the ratio of any two coefficients in the balanced equation is fixed. The only freedom for changing the balanced equation is multiplying all coefficients with the same factor. As an example, the complete combustion of butane is taken again:

  2C₄H₁₀ + 13O₂  →  8CO₂ + 10H₂O

This equation can be restated, e.g.

  4C₄H₁₀ + 26O₂  →  16CO₂ + 20H₂O     or    6C₄H₁₀ + 39O₂  →  24CO₂ + 30H₂O

or even with the use of fractions:

  C₄H₁₀ + 6½O₂  →  4CO₂ + 5H₂O

But all of these equations are equivalent. If any two coefficients are taken, then their ratio is the same for all equations. For example coefficient(butane) : coefficient(water) = 2 : 10 = 4 : 20 = 6 : 30 = 1 : 5.

An example of a reaction with a two dimensional solution space

However, there are reactions, for which no unambiguous balanced equation exists! These reactions certainly are not rare. Here, a reaction is presented, which is very common. It is the reaction between copper metal and nitric acid, with formation of copper (II) nitrate, nitrogen monoxide and nitrogen dioxide. This reaction is presented here in order to demonstrate some theory and how chemeq.exe can be used to analyse this kind of reactions.

The unbalanced reaction equation is: Cu + HNO₃  →  Cu²⁺ + NO₃^– + NO + NO₂ + H₂O

In this reaction, the liquid becomes blue, due to dissolved copper nitrate (Cu²⁺ ions and NO₃^– ions) and a mix of nitrogen oxides is produced. Besides that, also water is produced, but that cannot be observed.

When one tries to balance this equation, then a problem arises. It can be balanced in many different ways and now the different equations are not equivalent. Here, a few examples are given:

     Cu + 4HNO₃  →  Cu²⁺ + 2NO₃^– + 2NO₂ + 2H₂O

     2Cu + 6HNO₃  →  2Cu²⁺ + 4NO₃^– + NO + NO₂ + 3H₂O

     5Cu + 16HNO₃  →  5Cu²⁺ + 10NO₃^– + 2NO + 4NO₂ + 8H₂O

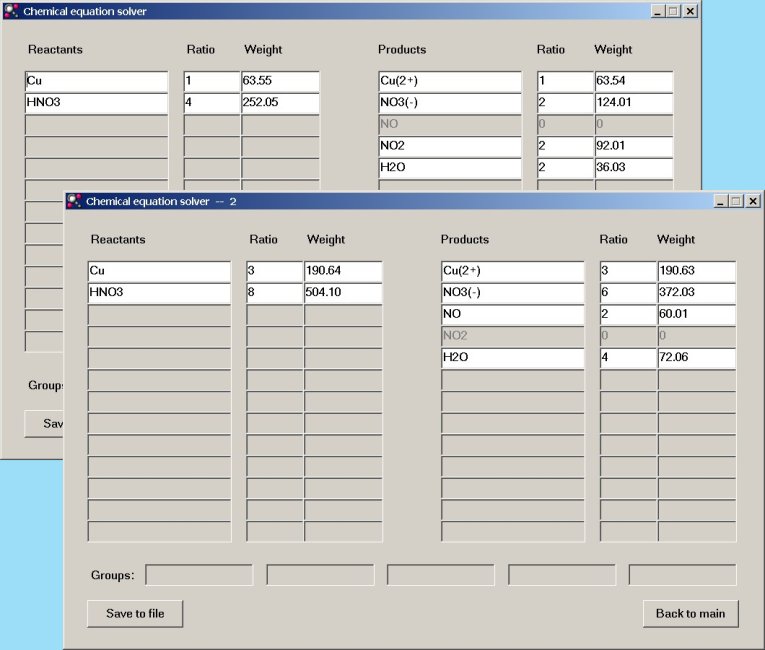
These examples are not simply equivalent versions, the only difference being a multiplying factor. Ratios of coefficients are not the same for these equations. For example, coefficient(copper) : coefficient(nitric acid) differs for all of these balanced equations. If such an ambiguity exists for the balanced equation, then that is an indication of different independent reactions, which can occur simultaneously. In this case, these two reactions are:

     Cu + 4HNO₃  →  Cu²⁺ + 2NO₃^– + 0 NO + 2NO₂ + 2H₂O

     3Cu + 8HNO₃  →  3Cu²⁺ + 6NO₃^– + 2NO + 0 NO₂ + 4H₂O

What actually happens depends on the precise reaction conditions, such as temperature, concentration of acid and how finely the metal is divided. Here, there are two independent reactions, and the observed reaction can be any combination of these two reactions. Mathematically speaking, the observed reaction can be any linear combination of the two independent reactions. All three balanced reaction equations for copper and nitric acid, given at the start of this section, can be derived from these two independent reaction by taking a constant times the first independent reaction plus another constant times the second independent reaction. E.g. the second reaction from the triple, given above, can be obtained as follows:

       Cu + 4HNO₃  →   Cu²⁺  + 2NO₃^–   +   0 NO  + 2NO₂    + 2H₂O             × 0.5

     3Cu + 8HNO₃  →  3Cu²⁺ + 6NO₃^–   +   2NO   + 0 NO₂   + 4H₂O             × 0.5

----------------------------------------------------------------------------------------------------------

     2Cu + 6HNO₃  →  2Cu²⁺ + 4NO₃^–   +   NO     +    NO₂  +  3H₂O

Any valid balanced equation is a combination of the two independent ones:

       Cu + 4HNO₃  →   Cu²⁺  + 2NO₃^–   +   0 NO  + 2NO₂    + 2H₂O             × a₁

     3Cu + 8HNO₃  →  3Cu²⁺ + 6NO₃^–   +   2NO   + 0 NO₂   + 4H₂O             × a₂

----------------------------------------------------------------------------------------------------------

     Every valid equation is of the form     a₁ × equation1 + a₂ × equation2

A reaction, which has two of such independent balanced equations, from which all other balanced equations can be derived is said to have a two-dimensional solution space. All reactions with unambiguous balanced equations (apart from a factor) are said to have a one-dimensional solution space. There also are reactions with even higher dimensional solution spaces.

The program chemeq.exe detects the presence of a higher dimensional solution space and it presents multiple solutions to the problem. The user is warned that the solution space is multi-dimensional, and after the warning multiple windows are shown, each window presenting a single independent solution.

When the two reactants in the copper/nitric acid reaction are typed at the left in chemeq.exe and the five products are typed at the right in the products column, then the program gives a popup message when the "Solve equation" button is pressed, indicating that it is not possible to derive an unambiguous balanced equation. The reaction usually has indeterminate stoichiometry, the only restriction being that it is a linear combination of multiple independent solutions.

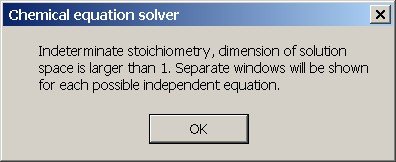
When the popup window is dismissed, then two windows appear, each with a possible independent solution.

Preservation of groups, influence on equation balancing

Even nastier balanced reaction equations exist as the ones with multi-dimensional solution spaces. There also are reaction equations, which definitely can be balanced unambiguously, but only by using additional knowledge, being that certain groups are preserved.

A nice example of such an equation is the well-known haloform reaction, e.g. for making iodoform from iodine, sodium hydroxide and acetone. The balanced reaction equation is as follows:

   CH₃COCH₃ + 3I₂ + 4OH^– → CH₃COO^– + 3I^– + 3H₂O + CHI₃

When the reactants and products are entered in chemeq.exe, then two independent reactions are given as answer:

(A)   2CH₃COCH₃ + 4I₂ + 11OH^– →  3CH₃COO^–  + 8I^– + 7H₂O + 0 CHI₃

(B)    CH₃COCH₃  + 5I₂ +  OH^–   → 0 CH₃COO^–   +  I^–  + 2H₂O + 3CHI₃

The above (and only possible) equation can be derived from these two independent equations, by taking ⅓A + ⅓B. But, based on the solution, provided by chemeq.exe, one could also end up with many other solutions, which in reality do not occur. So, although the solution space seems to be 2-dimensional, in reality it only is 1-dimensional. The reason for this is that an additional constraint must be imposed on the balanced equation. One of the CH₃-groups of the acetone is preserved in the reaction, it is not broken down, nor are any H-atoms replaced by I-atoms on that group. So, a better description of this reaction is:

   RCOCH₃ + 3I₂ + 4OH^– → RCOO^– + 3I^– + 3H₂O + CHI₃,   where R = CH₃.

Of course, this kind of knowledge cannot be derived by a computer program. It is the science of chemistry, which provides us with this kind of knowledge. Indeed, the haloform reaction works for any R. E.g. when R = H, then formiates are formed instead of acetates.

Using this knowledge, we can use chemeq.exe again, for balancing the equation. We enter the reactants and the products in the boxes, but we use the letter R instead of CH₃. Again, a new "element" is introduced, just as with the isotopes, but now, the "element" is defined as a group of already known elements, instead of a number, which tells its atomic mass. Below, the window is shown, with the introduction of the group R highlighted. The single and unambiguous solution now is derived without problem.

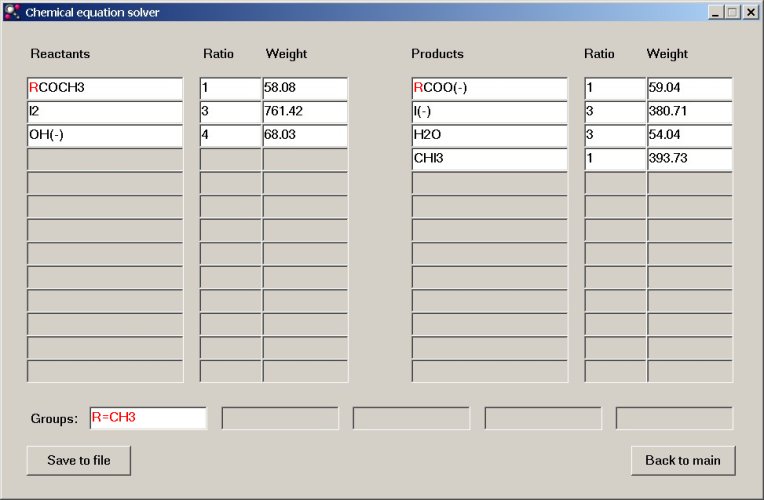
Of course, in the real program the input just is in black characters, here it is only shown for highlighting purposes.

If the group R would not be introduced, but instead of R, one simply types "CH3" in the reactants and products boxes, then the program tells there are two independent solutions. The program then does not know that it needs to preserve the CH₃-group.

When a group is introduced, then it really is handled like a real element. The total weight of the group is taken into account and it must appear in the reactants and products. If for instance, the group R is introduced, and it is used in the reactants, but in the products "CH3" is typed, then the program gives an error, indicating that element R is not present at both sides.

Also, when groups are defined in a box, then these groups may in turn be used in another box. Group definitions are created from left to right in the 5 group boxes. A group, defined in a certain box, can be used in group boxes, at the right. E.g., the following is valid:

Group Et uses the known groups R and R'. Group R* uses the known isotope C*. The order of group definitions may not be reversed. The definition of Et cannot be at the left of the definition of R or R'. If one does so, then chemeq.exe will tell that group Et uses an unknown element.

back to top of page

back to main chemeq page

back to miscellaneous main page