Chemical equation solver - getting started

In this page, a short introduction to the webpage for solving chemical equations is given, such that you can use the webpage quickly without a steep learning curve. Just follow the examples. In the tutorial below, the webpage simply is called chemeq. Point the browser to the right location by typing the URL of the webpage in the web browser address bar.

Basics: balancing an equation

The primary goal of the website is to balance equations. This can be done very easily. In order to show how to do this, a somewhat less trivial example is given: the oxidation of sulphur dioxide by dichromate ion in acidic media, giving trivalent chromium ions and sulfate ions. This is a common redox reaction, often encountered in high-school chemistry textbooks.

The unbalanced equation for this is:

    Cr₂O₇^2- + SO₂ + H⁺  →  Cr³⁺ + SO₄^2- + H₂O

In order to balance this equation, we simply type the reactants and products in chemeq, each reactant and product in a single box. Ionic charges are given between parentheses.

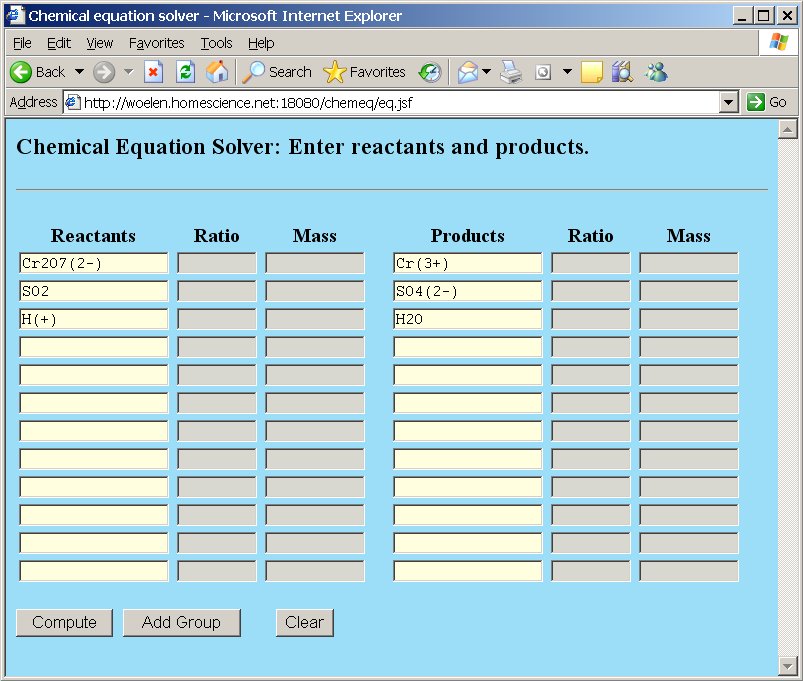
Next, click the "Compute" button and when this is done, the browser window is redrawn, with the coefficients in the ratio-columns and the total molecular weight in the weight column. So, the equation is balanced and the correct equation becomes:

    Cr₂O₇^2- + 3SO₂ + 2H⁺  →  2Cr³⁺ + 3SO₄^2- + H₂O

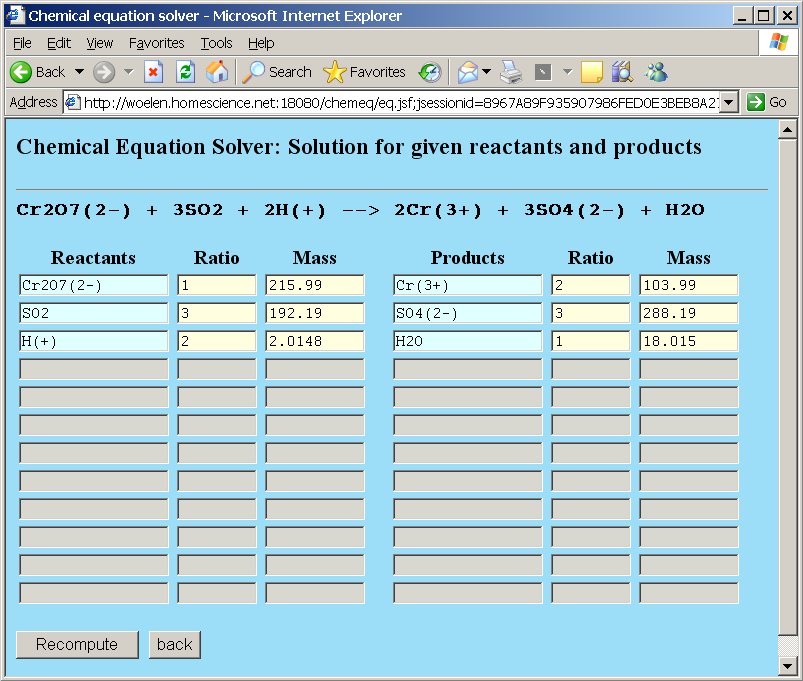
By clicking the "back" button you go back to the initial page, in which reactants and products can be edited. By clicking the "clear" button all reactants and products are removed and a new chemical equation can be balanced.

Basics: use as very simple molecular mass calculator

Sometimes one just wants the molecular mass of a single compound. Chemeq can also be used for such computations. One simply types the formula of the compound in one of the reactants boxes at the left and then the "Compute" button is clicked. Only one box may be filled with a formula when chemeq is used as simple molecular mass calculator. As soon as more boxes are filled, then the webpage does not work in this special mode anymore.

When the "Compute" button is clicked, then a new window appears, with the total molecular mass of the compound in the reactants mass column. The mass of each element in the compound is displayed in the product mass column.

In this mode, the webpage actually solves the equation, where the compound is completely decomposed into its elements.

Basics: determining half reactions for redox reactions

A very common thing, needed for determining how redox reactions proceed, are the so-called half-reactions. These frequently are tabulated, together with a redox potential. Many people try to memorize these kinds of reactions, but chemeq is capable of deriving them. What needs to be known is the input compounds or ions, the number of electrons consumed or produced, and the output compounds or ions. The webpage then determines the fully balanced half-reaction.

Some examples: dichromate, acting as oxidizer in acidic media, hence "consumption" of electrons.

Input: Cr₂O₇^2-, H⁺, e

Output: Cr³⁺, H₂O

This problem simply can be solved by typing Cr2O7(2-), H(+) and e in the reactants column and typing Cr(3+)and H2O in the products column. The result is as follows:

   Cr₂O₇^2- + 14H⁺ + 6e  →  2Cr³⁺ + 7H₂O

This is a well-known and frequently tabulated reaction. Things become more interesting when a much less common half-reaction needs to be derived.

As an example we use the half-reaction from the brown hypovanadate to colorless orthovanadate in strongly alkaline solutions. Hypovanadate contains vanadium metal in the +4 oxidation state and has formula V₄O₉^2- and orthovanadate contains vanadium in the +5 oxidation state and has formula VO₄^3-. The vanadium obtains a higher oxidation state and hence is reduced. It "produces" electrons. The reaction occurs in strongly alkaline environments, so we need hydroxide ion for compensation of oxygen. We do not know in advance whether the reaction consumes or produces hydroxide ion. We just try with water as input and hydroxide as output:

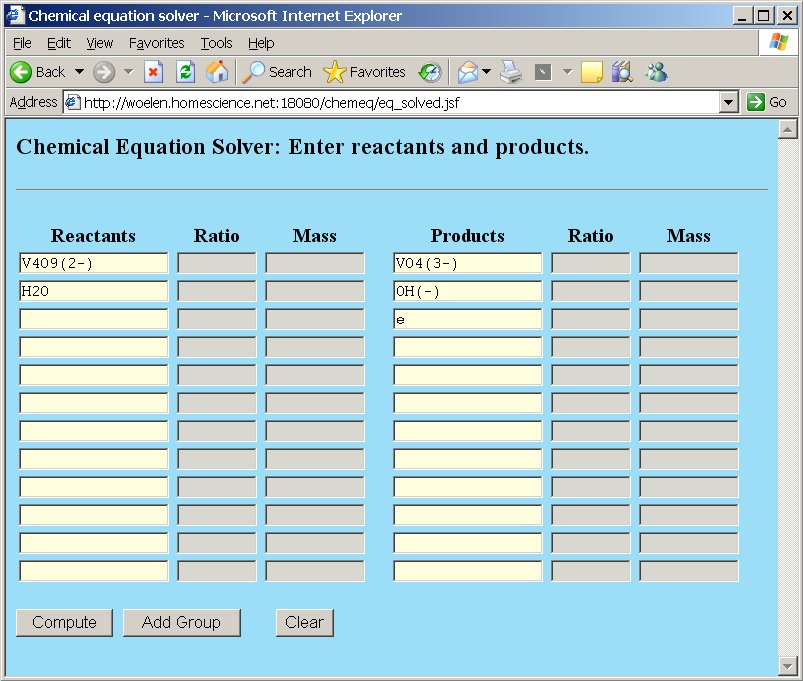
The result of this is given by chemeq as follows, when the "Compute" button is clicked:

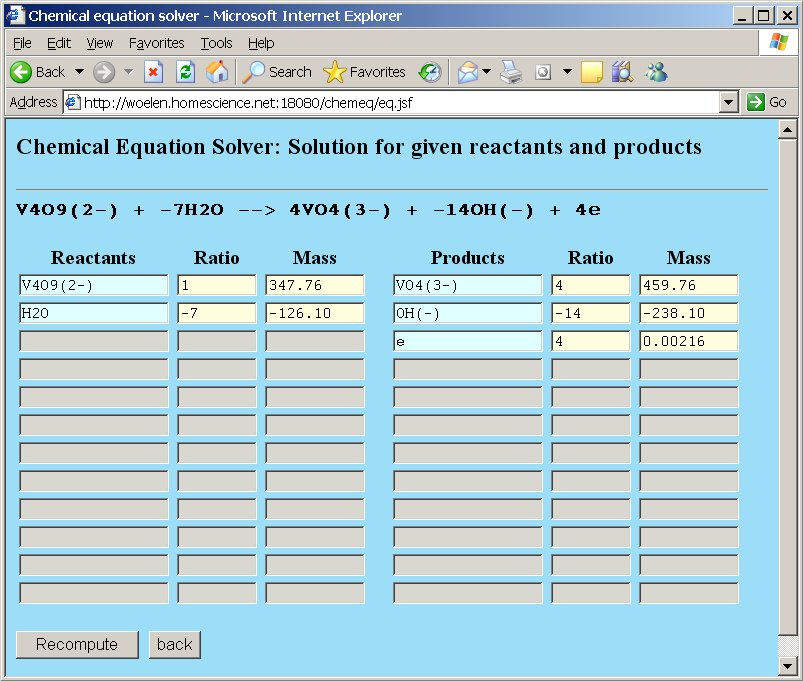
   V₄O₉^2- − 7H₂O  →  4VO₄^3- − 14OH⁻ + 6e

Chemeq shows that water and hydroxide has negative coefficients. These need to be reversed. Click the "back" button in the window and put hydroxide ion at the left in the reactants column and water at the right in the products column in order to get a correct equation:

   V₄O₉^2- + 14OH⁻  →  4VO₄^3- + 7H₂O + 6e

In this way, chemeq can be used easily to derive half-equations for reduction or oxidation.

Basics: doing some automated computations

In this example we are studying the complete combustion of butane gas. The reaction products are water and carbon dioxide. The unbalanced equation for this is:

   C₄H₁₀ + O₂  →  CO₂ + H₂O

Again, we type the reactants and products, and we click the "Compute" button:

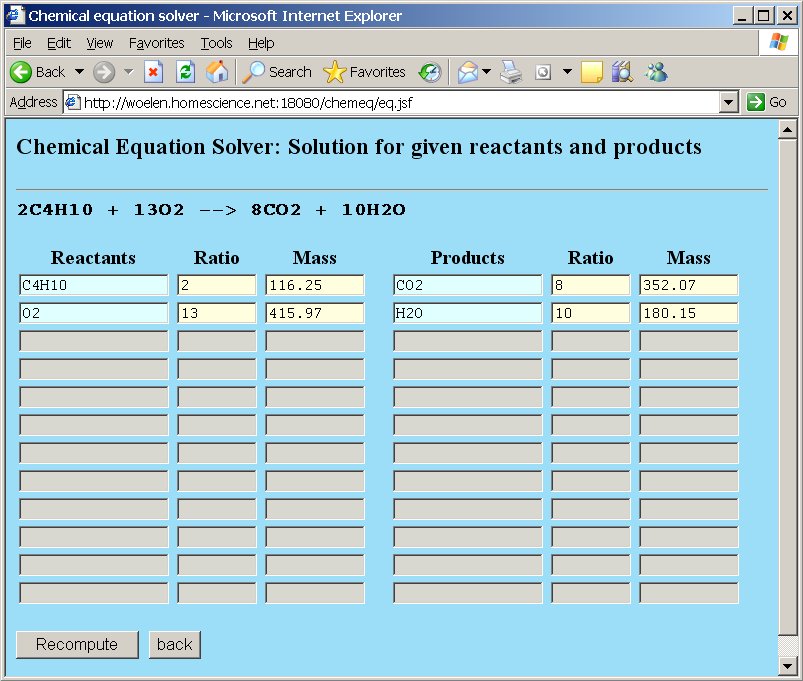
This gives the following result, which allows us to balance the equation:

   2C₄H₁₀ + 13O₂  →  8CO₂ + 10H₂O

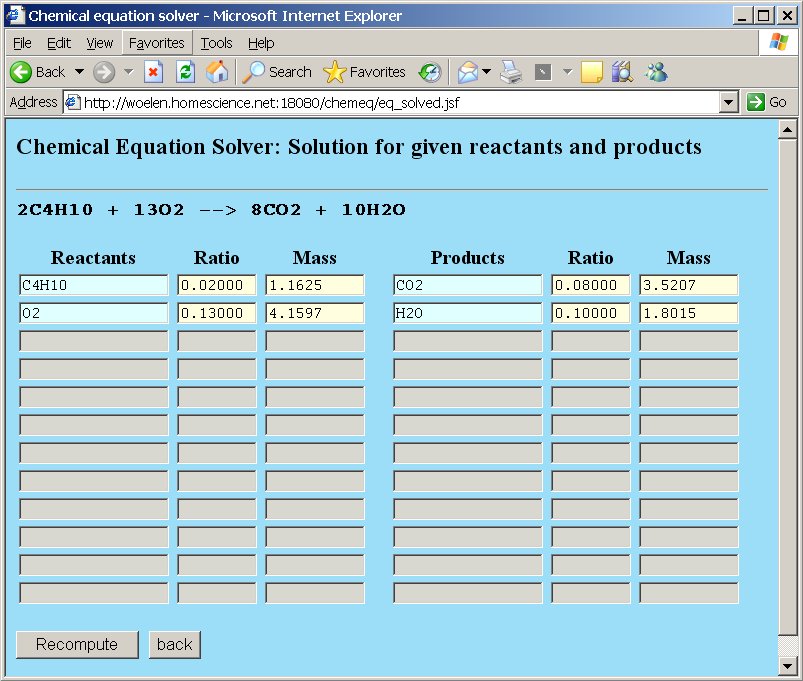
The webpage, however, allows us to do more than simple balancing of equations. Suppose we are asked the question "How many grams of oxygen and how many moles of oxygen are needed for complete combustion of 10 grams of butane gas?". This question can very simply be solved. At the molecular mass field for butane replace the number 116.25 by the assignment =10. The total mass of butane is set to 10 grams. The webpage can recompute all other quantities, such that the overall stoichiometric ratios are still correct. After editing the total mass of butane press the "Recompute" button or press enter.

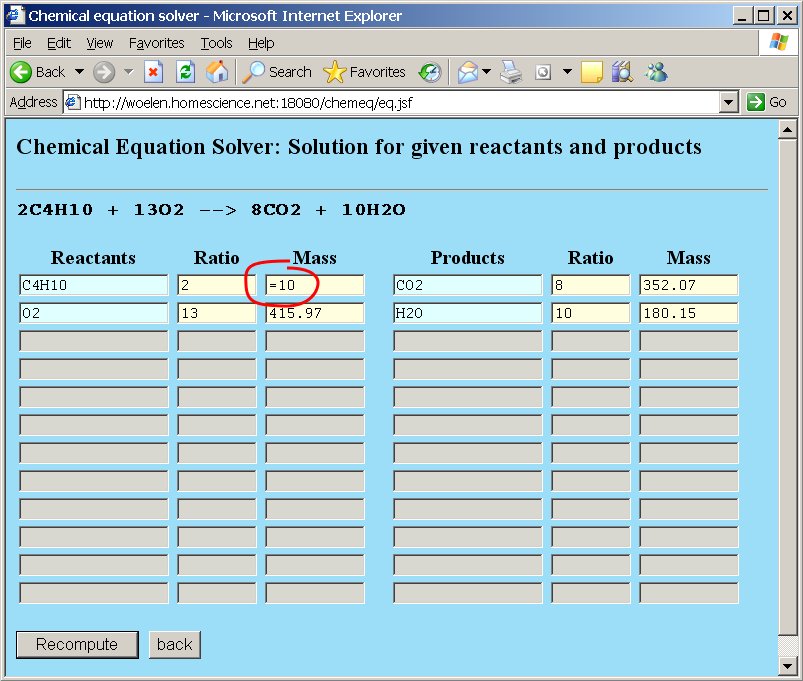
The other numeric values are adjusted:

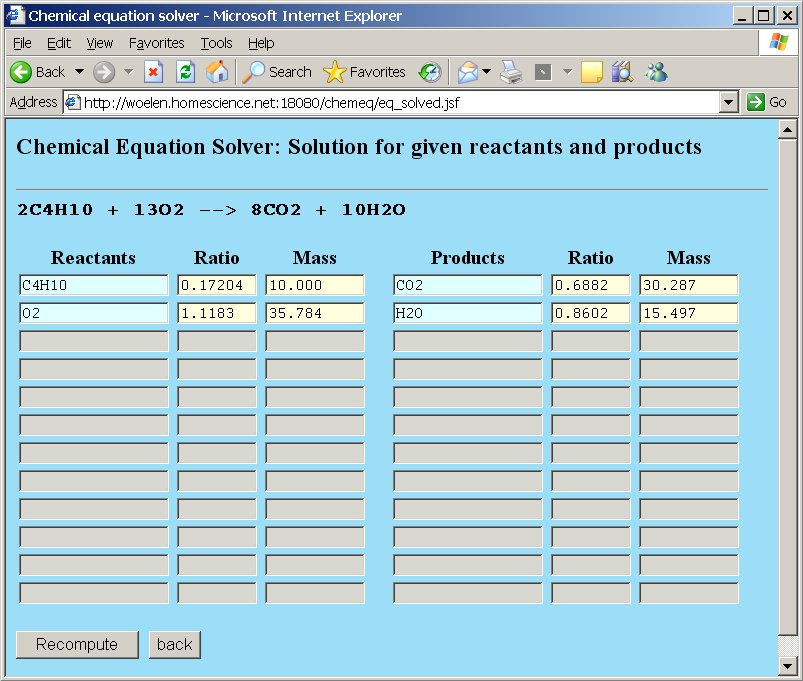
So, when 10 grams of butane are used, then 35.784 grams of oxygen are needed, which equals 1.1183 moles of oxygen molecules O₂.

Now, suppose that we are asked the question: "How many grams of butane are needed to produce 0.1 mol of water?". In order to do so, we edit the "Ratio" box for water and type the assignment =0.1.

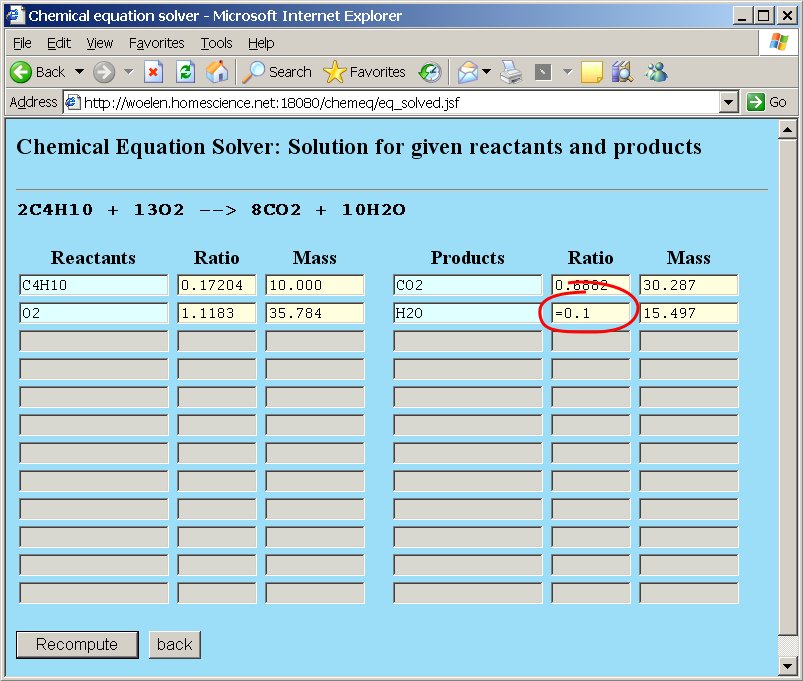
All other values are updated again when the "Recompute" button is clicked. The answer to this question is 1.1625 grams of butane:

An assignment of a mass or a ratio always must be of the form =<number>. Any other input is rejected and leads to an error message. Another rule is that only one number can be replaced by an assignment. Multiple assignments usually lead to conflicting situations, because the recomputation due to one assignment usually does not match the given value of the other assignment(s). So, if more than one assignment is given and then the "Recompute" button is clicked, this also leads to an error message.

Groups: Introduction of isotopes, structural groups and 'fantasy elements'

Up to now, no special elements have been used. Chemeq, however, also supports working with isotopes of the existing elements, or even virtual elements with any atomic mass. This is where the "Add Group" button of the main page comes into play. In this page you can define new 'elements' with a symbol and a value. Such an element is called a 'group' in chemeq. Three types of groups are supported:

• Existing isotopes of the existing elements
• Structural groups which are known to be preserved in chemical reactions
• 'Fantasy' elements with arbitrary mass

These groups can be defined in the groups page. The groups page appears when the "Add Group" button on the main page is clicked:

Below, some examples of possible inputs are shown:

The first example introduces an element with symbol C' as the ¹⁴C isotope of carbon. All known isotopes can be introduced. The symbol does not need to be like C' for isotopes of carbon, any other syntactically valid symbol (see below for syntax rules) may be used, so the following is equally valid: Iso = C:14. When this is used, the symbol Iso must be used in chemical equations instead of C'.

The second example introduces the ethyl group, and once this is used, one can use the symbol Et in chemical equations. This symbol then must be used in the reactants and in the products, it is preserved (for more on this topic see further below).

The third example introduces a fantasy super-heavy element with a molar mass of 1020.67 g/mol.

In general, the syntax for addition of a group is either one of the following three:

• <symbol> = <element>:<isotope number> --- this syntax with a colon, at the left an existing element and at the right an integer number, introduces an existing isotope and assigns this to the symbol at the left of the assignment. Only existing isotopes can be selected in this way, e.g. S:34 is a valid value, but S:35 is not a valid value (³⁴S exists, ³⁵S does not exist). If an attempt is made to add a nonexistent isotope, then an error message is presented and the list of groups is not changed.
• <symbol> = <formula> --- this syntax requires a valid radical or molecule formula at the right side of the assignment. The valid formula only has to be syntactically correct, if it is meaningless from a chemical point of view, then still it is accepted.
• <symbol> = <positive number> --- this syntax allows one to create an element with any molar mass. This can be useful for highly specialized computations, where one wants to perform computations with special non-existent isotopes or special groups, of which the mass is known, but the structure is unknown. For most general work, the first two options are sufficient.

The symbol for these groups must start with a capital letter, and optionally two other characters can be added. These characters may be any lowercase letter, a ' or a *, digits are not allowed. Some examples of valid and invalid symbols:

• Valid symbols: Own, C', C'', Mmm, Mm, O*, Se*, O*', O'*, Lol, L*l.
• Invalid symbols: OWn, CC, C*L, LoL, C14, Se2.

Once you are finished adding groups, you can click the "back" button, which brings you back to the main page. Now you can use the newly introduced symbol in chemical formulas in the reactants and products and do chemistry equation solving and mass computations on these as well, besides the standard elements.

An isotope example with ¹⁴C

An example demonstrates the usefulness of groups. Suppose we have the example of combustion of butane, but instead of plain carbon, the butane is partially based on the special ¹⁴C isotope, one of the carbon atoms is the ¹⁴C isotope, the other carbon atoms are plain carbon. Now, we are going to study the combustion of C₃C'H₁₀, where C' is the ¹⁴C isotope of carbon.

When a new isotope is added, then of course, the reactants and reaction products must also be changed accordingly. In the example with combustion of butane, two types of molecules of carbon dioxide will be formed, one type with the special isotope and the other type with normal carbon. The following reactants and products are involved in the reaction:

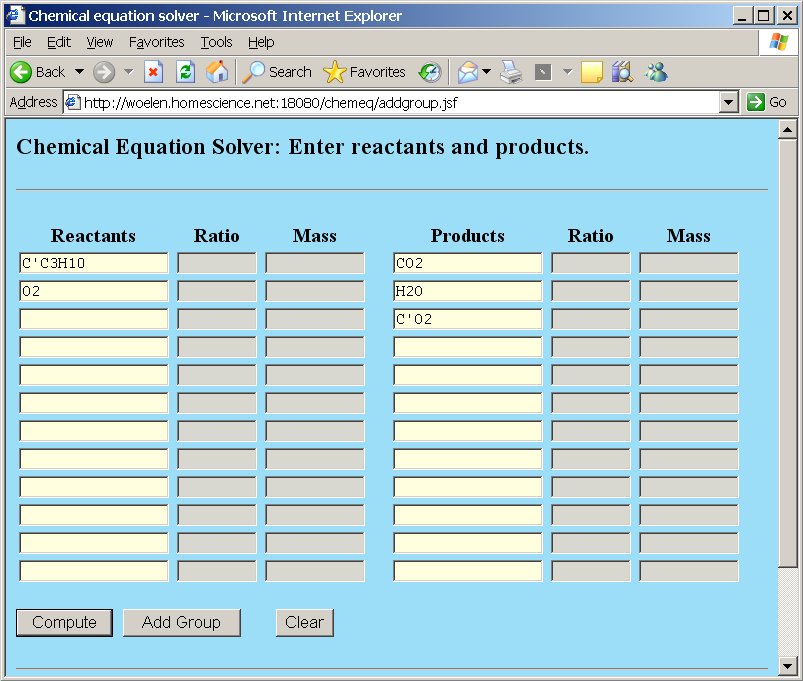
Now, if the "Compute" button is clicked, the equation is balanced, and the newly added isotope C' is perfectly treated as a separate element, which is preserved, just like the other elements.

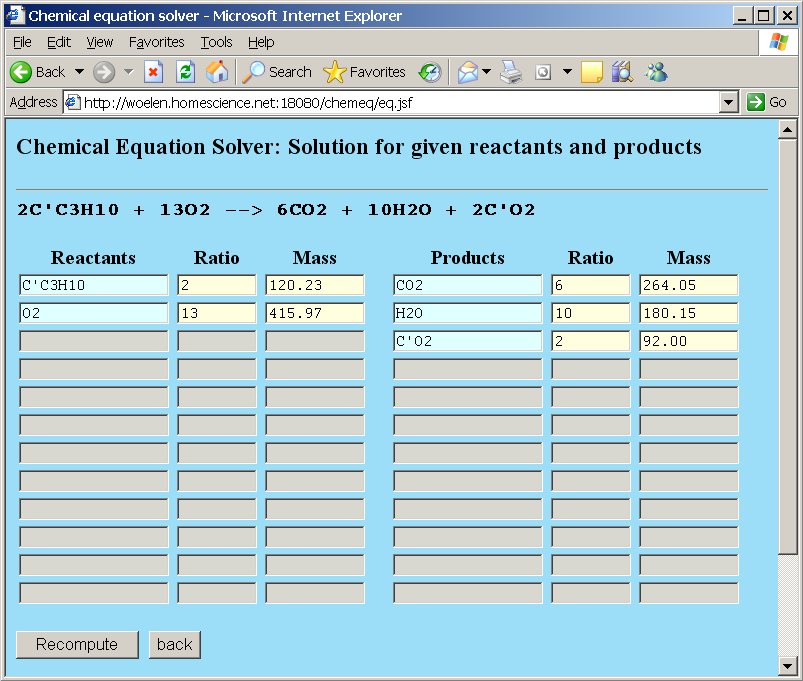
As with the previous example with normal butane, you can also recompute molar masses and molar ratios of the reactants and products by putting an assignment in one of the boxes and clicking the "Recompute" button.

Reminder display for added groups

Each group, which is added, is displayed on all pages as a reminder. Suppose one adds the groups Et = CH3CH2 and Fan = 1234.56, then this looks as follows in the main page and group page.

Main page, with a reaction in which the Et-group is preserved. The list of available groups is displayed at the bottom of the screen. The example shows the window, scrolled down to the bottom.

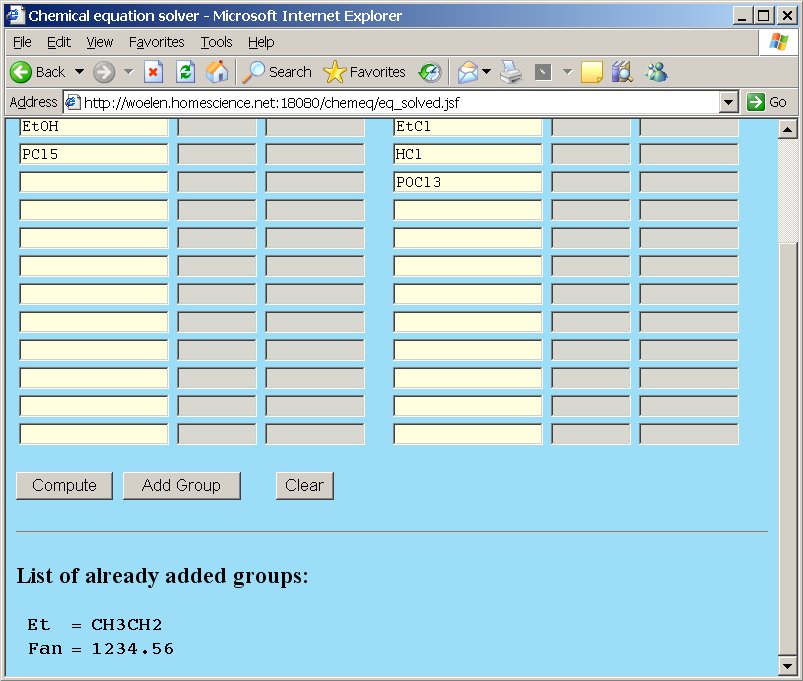
Group page, showing the same two groups:

Removal of groups

If in the group page the "Clear All" button is clicked, then all groups are removed. This does not clear the main page. If the "Clear All" button on the group page is clicked, and then the "Back" button is clicked, then the resulting page still holds the reactants and products. If these still contain symbols, assigned in the groups and then the "Compute" button is clicked, then an error message is produced:

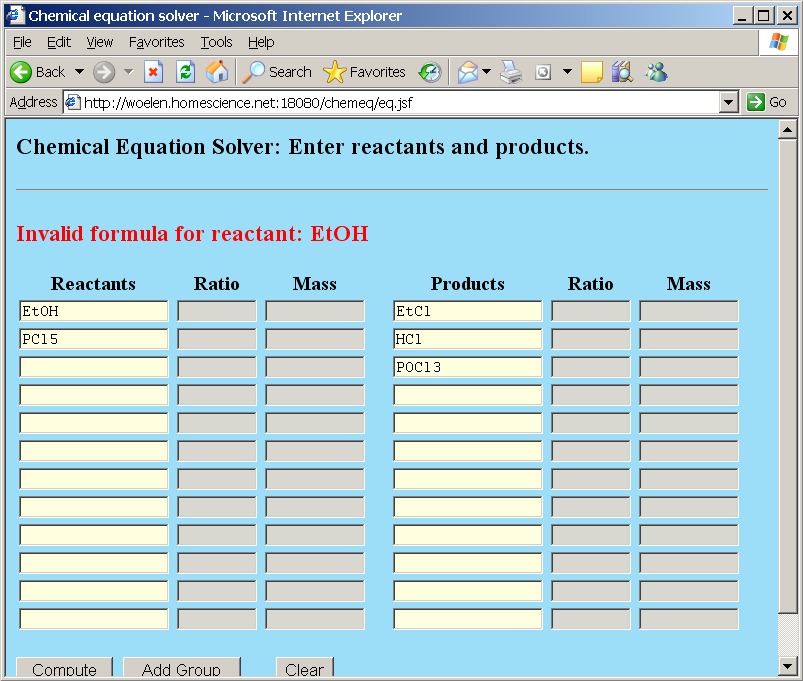
The formula EtOH is not a valid formula anymore, because Et is not a known element, nor a known group anymore.

Nested group definitions

Definitions of groups may be nested. When a new group is defined, then in the new group, already known groups can be used. An example is the following:

First, one defines Me = CH3, and next, one defines Et = MeCH2. One cannot first define the group Et = MeCH2 and then Me = CH3, because the group Me is not (yet) known.

Advanced issues: multidimensional solution spaces and grouping

Most chemical reactions could be covered quite well by chemeq, if it had only the functionality, as described above. However, there also is a whole class of reactions, which cannot be balanced unambiguously. It is said that an equation can be balanced unambiguously, if the ratio of any two coefficients in the balanced equation is fixed. The only freedom for changing the balanced equation is multiplying all coefficients with the same factor. As an example, the complete combustion of butane is taken again:

  2C₄H₁₀ + 13O₂  →  8CO₂ + 10H₂O

This equation can be restated, e.g.

  4C₄H₁₀ + 26O₂  →  16CO₂ + 20H₂O     or    6C₄H₁₀ + 39O₂  →  24CO₂ + 30H₂O

or even with the use of fractions:

  C₄H₁₀ + 6½O₂  →  4CO₂ + 5H₂O

But all of these equations are equivalent. If any two coefficients are taken, then their ratio is the same for all equations. For example coefficient(butane) : coefficient(water) = 2 : 10 = 4 : 20 = 6 : 30 = 1 : 5.

An example of a reaction with a two dimensional solution space

However, there are reactions, for which no unambiguous balanced equation exists! These reactions certainly are not rare. Here, a reaction is presented, which is very common. It is the reaction between copper metal and nitric acid, with formation of copper (II) nitrate, nitrogen monoxide and nitrogen dioxide. This reaction is presented here in order to demonstrate some theory and how chemeq can be used to analyse this kind of reactions.

The unbalanced reaction equation is: Cu + HNO₃  →  Cu²⁺ + NO₃⁻ + NO + NO₂ + H₂O

In this reaction, the liquid becomes blue, due to dissolved copper nitrate (Cu²⁺ ions and NO₃⁻ ions) and a mix of nitrogen oxides is produced. Besides that, also water is produced, but that cannot be observed.

When one tries to balance this equation, then a problem arises. It can be balanced in many different ways and now the different equations are not equivalent. Here, a few examples are given:

     Cu + 4HNO₃  →  Cu²⁺ + 2NO₃⁻ + 2NO₂ + 2H₂O

     2Cu + 6HNO₃  →  2Cu²⁺ + 4NO₃⁻ + NO + NO₂ + 3H₂O

     5Cu + 16HNO₃  →  5Cu²⁺ + 10NO₃⁻ + 2NO + 4NO₂ + 8H₂O

These examples are not simply equivalent versions with the only difference being a multiplying factor. Ratios of coefficients are not the same for these equations. For example, coefficient(copper) : coefficient(nitric acid) differs for all of these balanced equations. If such an ambiguity exists for the balanced equation, then that is an indication of different independent reactions, which can occur simultaneously. In this case, these two reactions are:

     Cu + 4HNO₃  →  Cu²⁺ + 2NO₃⁻ + 0 NO + 2NO₂ + 2H₂O

     3Cu + 8HNO₃  →  3Cu²⁺ + 6NO₃⁻ + 2NO + 0 NO₂ + 4H₂O

What actually happens depends on the precise reaction conditions, such as temperature, concentration of acid and how finely the metal is divided. Here, there are two independent reactions, and the observed reaction can be any combination of these two reactions. Mathematically speaking, the observed reaction can be any linear combination of the two independent reactions. All three balanced reaction equations for copper and nitric acid, given at the start of this section, can be derived from these two independent reactions by taking a constant times the first independent reaction plus another constant times the second independent reaction. E.g. the second reaction from the triple, given above, can be obtained as follows:

       Cu + 4HNO₃  →   Cu²⁺  + 2NO₃⁻   +   0 NO  + 2NO₂    + 2H₂O             × ½

     3Cu + 8HNO₃  →  3Cu²⁺ + 6NO₃⁻   +   2NO   + 0 NO₂   + 4H₂O             × ½

----------------------------------------------------------------------------------------------------------

     2Cu + 6HNO₃  →  2Cu²⁺ + 4NO₃⁻   +   NO     +    NO₂  +  3H₂O

Any valid balanced equation is a combination of the two independent ones:

       Cu + 4HNO₃  →   Cu²⁺  + 2NO₃⁻   +   0 NO  + 2NO₂    + 2H₂O             × a₁

     3Cu + 8HNO₃  →  3Cu²⁺ + 6NO₃⁻   +   2NO   + 0 NO₂   + 4H₂O             × a₂

----------------------------------------------------------------------------------------------------------

     Every valid equation is of the form     a₁ × equation1 + a₂ × equation2

A reaction, which has two of such independent balanced equations, from which all other balanced equations can be derived is said to have a two-dimensional solution space. All reactions with unambiguous balanced equations (apart from a factor) are said to have a one-dimensional solution space. There also are reactions with even higher dimensional solution spaces.

Chemeq detects the presence of a higher dimensional solution space and it presents multiple solutions to the problem. The user is warned that the solution space is multi-dimensional, and each single independent solution can be displayed as a single solution-set. Chemeq allows the user to select a solution set by clicking on the number of the solution set.

When the two reactants in the copper/nitric acid reaction are typed at the left in chemeq and the five products are typed at the right in the products column, then a page is presented with a warning, a display of solution set 1 and a link, which can be clicked for solution set 2:

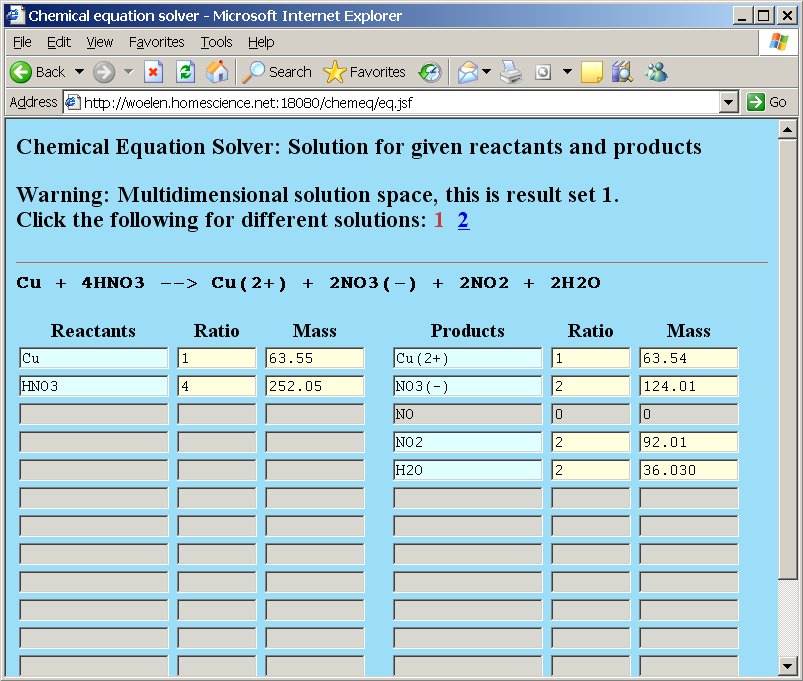
The currently displayed solution set is number 1 (the 1 is displayed in brick-red and cannot be clicked as a link). If you want to view the other solution set, then the link number 2 must be clicked. If that is done, then the following page appears:

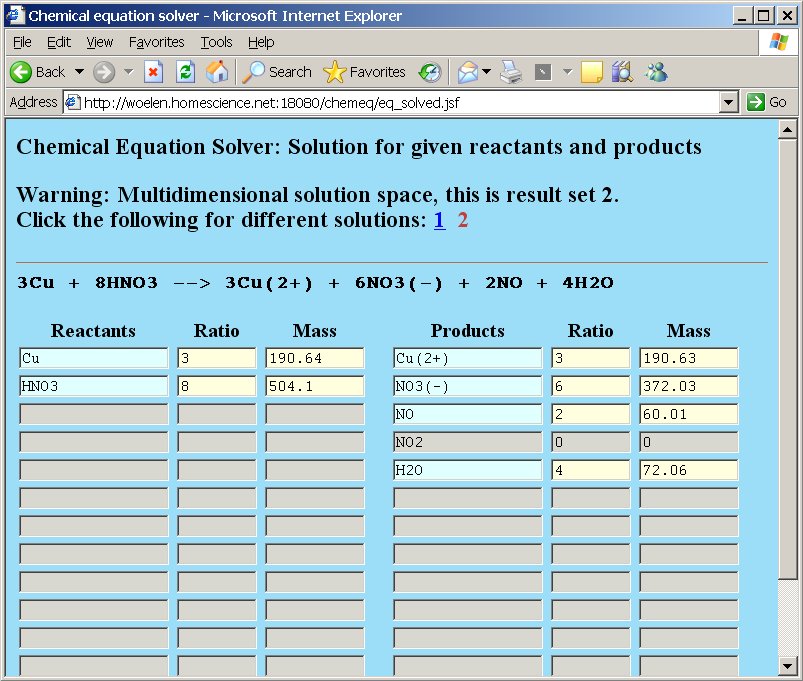
In both solution sets you can replace ratios and masses by means of assignments in order to do molar mass calculations and ratio calculations, as explained earlier. If such computations are done in a solution set, then they only affect that solution set. If e.g. the assignment =1 is placed in the ratio field of the copper reactants and the "Recompute" button is clicked, then the page is changed accordingly, but if after this recomputation the 1 link is clicked, then that page is not adjusted. If on that page the 2 link is clicked again, then the recomputed values from solution set 2 are displayed again. So, chemeq maintains recomputed state when the user switches between solution sets, but recomputation in one solution set does not affect ratios and masses in other solution sets. As soon as the "back" button is clicked in any solution set, then all recomputations are lost.

Preservation of groups, influence on equation balancing

Even nastier balanced reaction equations exist as the ones with multi-dimensional solution spaces. There also are reaction equations, which definitely can be balanced unambiguously, but only by using additional knowledge, being that certain groups are preserved.

A nasty example of such an equation is the well-known haloform reaction, e.g. for making iodoform from iodine, sodium hydroxide and acetone. The unbalanced equation is as follows:

   CH₃COCH₃ + I₂ + OH⁻ → CH₃COO⁻ + I⁻ + H₂O + CHI₃

A naive user would supply the following input in chemeq:

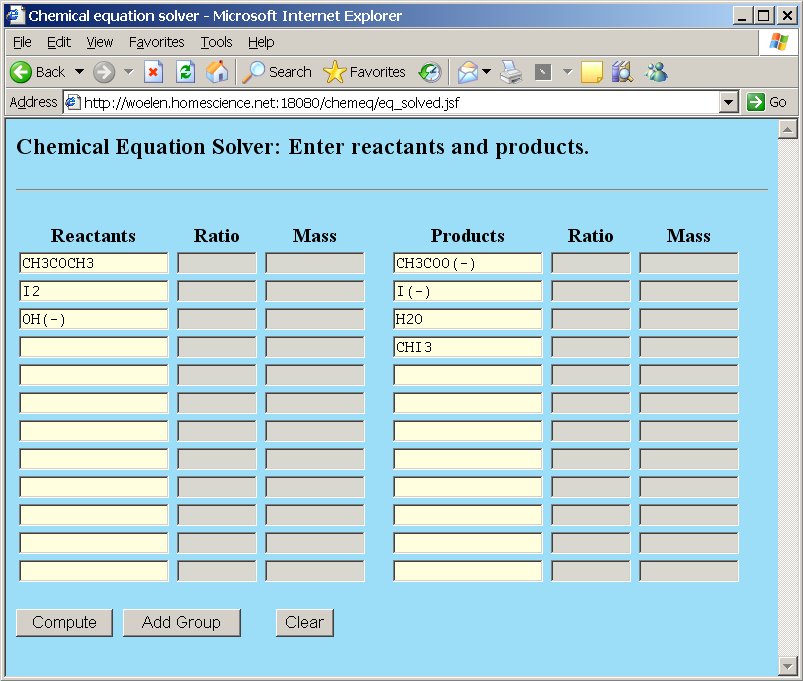
After pressing the "Compute" button, the webpage gives a result, telling that there are two solution sets and that the solution space is multidimensional. Below, both solution sets are shown:

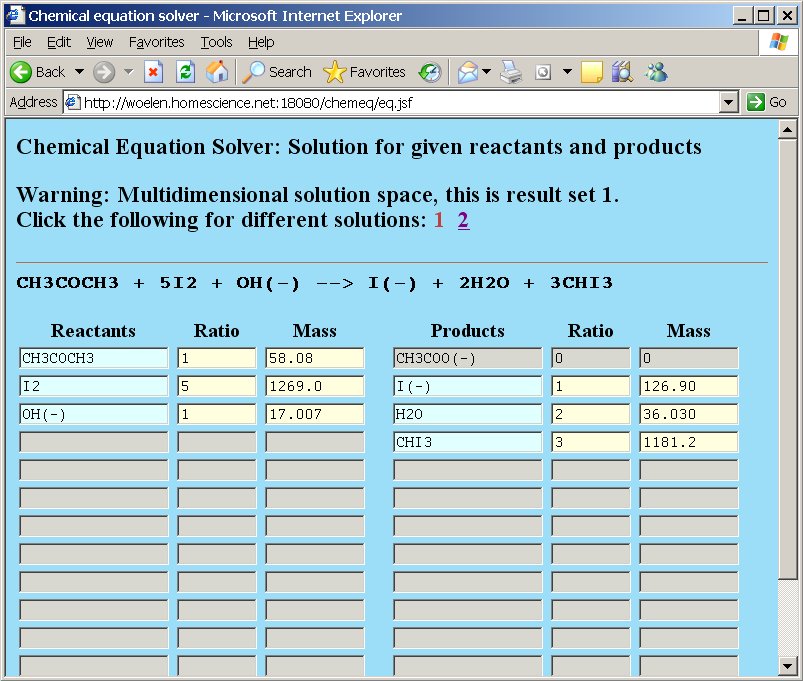
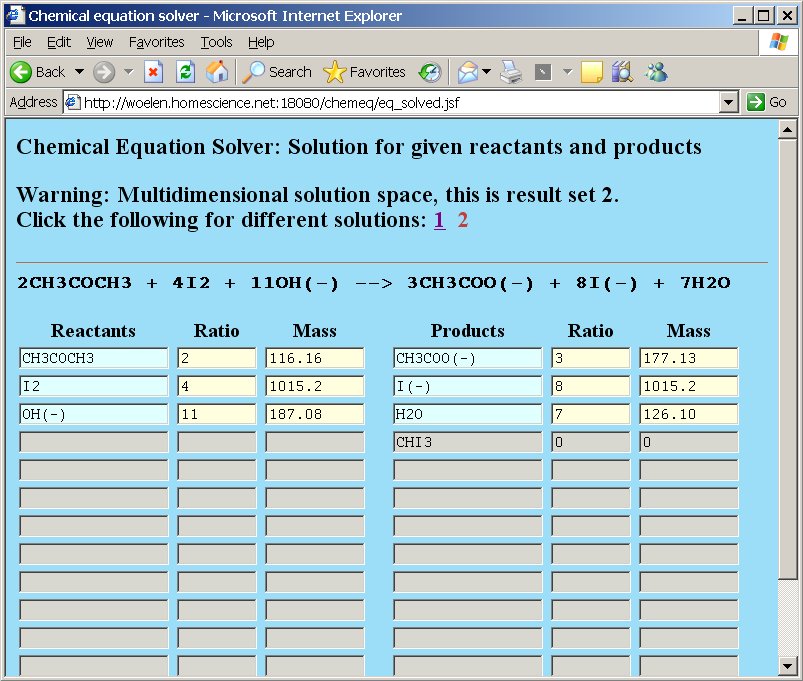
The output of chemeq corresponds to the two equations shown here.

(A)   2CH₃COCH₃ + 4I₂ + 11OH⁻ →  3CH₃COO⁻  + 8I⁻ + 7H₂O + 0 CHI₃

(B)    CH₃COCH₃  + 5I₂ +  OH⁻   → 0 CH₃COO⁻   +  I⁻  + 2H₂O + 3CHI₃

The correct balanced reaction equation, however, is as follows:

   CH₃COCH₃ + 3I₂ + 4OH⁻ → CH₃COO⁻ + 3I⁻ + 3H₂O + CHI₃

The correct (and only possible) equation can be derived from these two independent equations, by taking ⅓A + ⅓B. But, based on the solution, provided by chemeq, one could also end up with many other solutions, which in reality do not occur. So, although the solution space seems to be 2-dimensional, in reality it only is 1-dimensional. The reason for this is that an additional constraint must be imposed on the balanced equation. One of the CH₃-groups of the acetone is preserved in the reaction, it is not broken down, nor are any H-atoms replaced by I-atoms on that group. So, a better description of this reaction is:

   RCOCH₃ + 3I₂ + 4OH⁻ → RCOO⁻ + 3I⁻ + 3H₂O + CHI₃,   where R = CH₃.

Of course, this kind of knowledge cannot be derived by a computer program. It is the science of chemistry, which provides us with this kind of knowledge. Indeed, the haloform reaction works for any R. E.g. when R = H, then formiates are formed instead of acetates and when R is an ethyl group (in MEK), then propionates are formed instead of acetates.

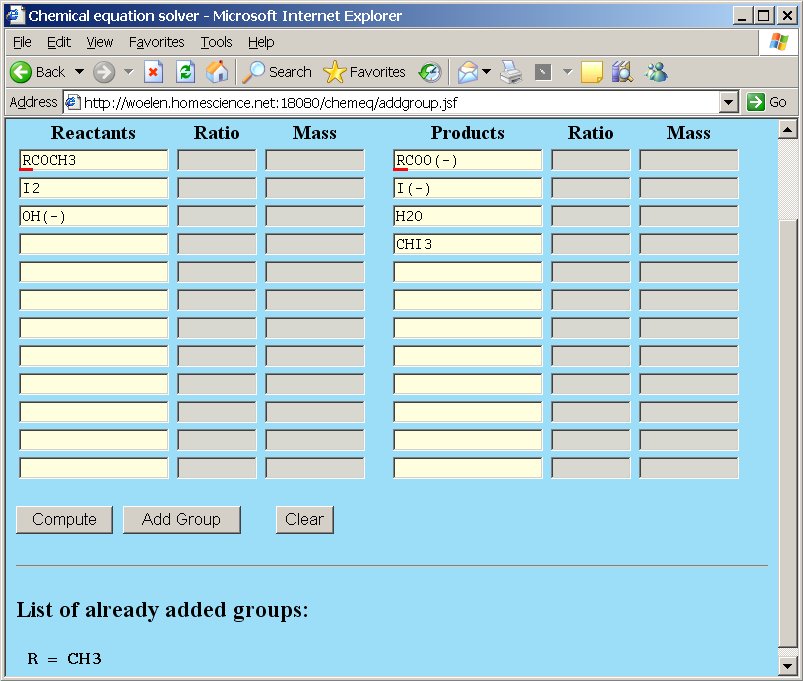
Using this knowledge, we can use chemeq again, for balancing the equation. We enter the reactants and the products in the boxes, but we use the group R instead of CH₃. We introduce a group R = CH3 in the group page by clicking the "Add Group" button and adding the group in that page (see above for more details about adding groups). In the main page we then enter the following (after the group is added).

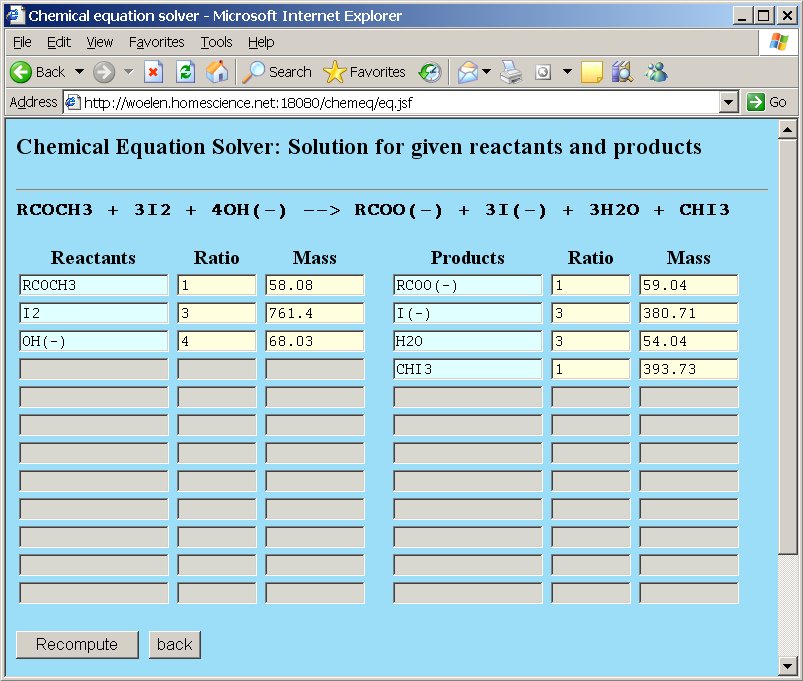
After clicking the "Compute" button, the single correct solution is presented.

If the group R would not be introduced, but instead of R, one simply types "CH3" in the reactants and products boxes, then chemeq does not know that it needs to preserve the CH₃-group.

When a group is introduced, then it really is handled like a real element. The total weight of the group is taken into account and it must appear in the reactants and products. If for instance, the group R is introduced, and it is used in the reactants, but in the products "CH3" is typed, then the webpage gives an error, indicating that element R is not present at both sides.